日本語/JP:https://www.cyberwei.com/archives/220810jp
1. 研究背景
图1
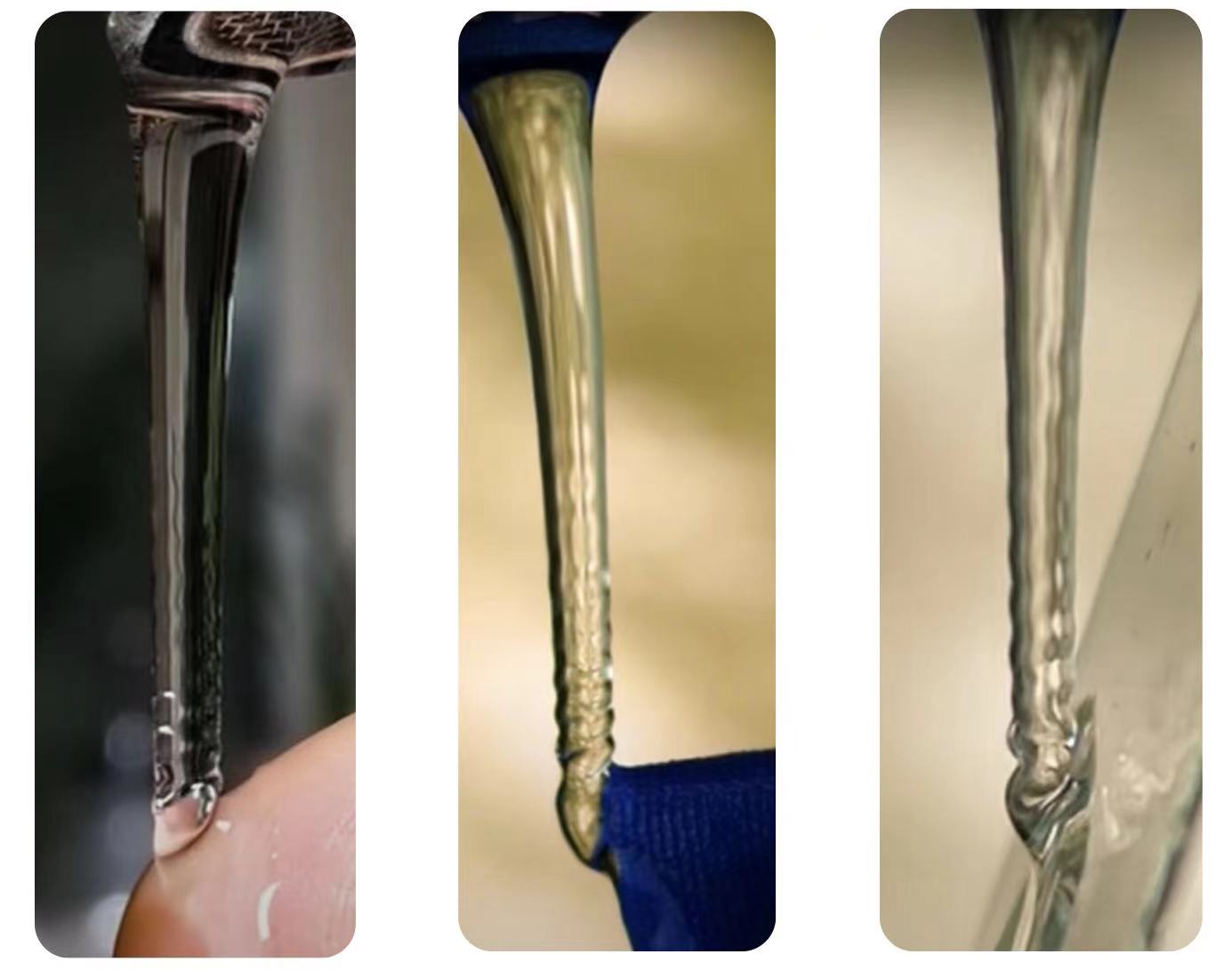
我们打开水龙头并调节使其形成较稳定的层流。可以观察到如下几个现象:首先液体柱的半径呈圆形,其半径随着下落高度的增加而缩小。并在某一特定高度下失去层流形态(破碎)后分散成若干水珠下落。此外,若我们使水流在破碎前与某一平面接触,水柱会吸附到该平面上流动。当我们仔细观察液体与平面接触点附近的水柱时,可以发现水柱在此处产生了某种波动现象,同时该波动呈现驻波形态。此外如果调整水流流量使其在接触面附近破碎,我们可以发现其破碎间隔与该驻波的波长十分接近。因此推断该现象与液体流下落破碎的产生机制相同。本研究将针对此条件下的液体柱波动现象进行建模分析。
2. 对现象的建模分析
图1展示了该波动的具体形态,该波动看上去是静止的。但众所周知水流在静止状态下并不会出现静止的波纹。所以我们不妨首先大胆假设该波动呈现静止的原因是液体下落速度与波动向上传播的速度相同。接下来我们将计算波动在水流柱表面的波动方程与其速度。
2.1. 自由下落水流的界面半径变化
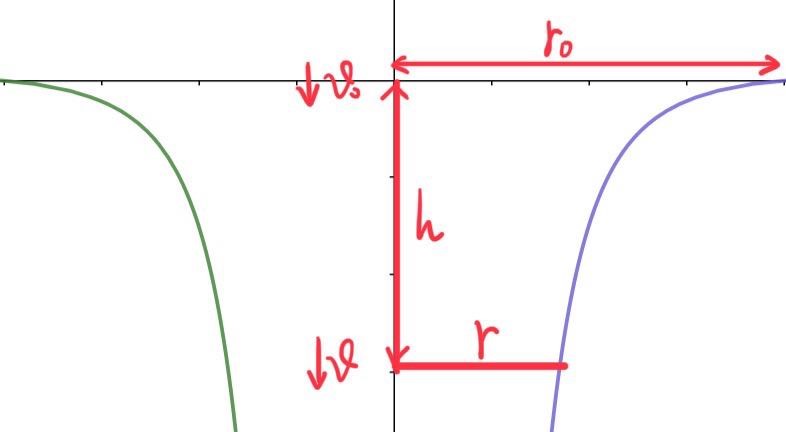
在具体计算水流柱振动之前首先来分析一下在水流下落过程中截面半径与下落高度之间的关系
图2
v d S = c o n s t (2.1.1) vdS=const\tag{2.1.1}
v d S = c o n s t ( 2 . 1 . 1 )
p + 0.5 ρ v 2 + ρ g h = c o n s t (2.1.2) p+0.5ρv^2+ρgh=const\tag{2.1.2}
p + 0 . 5 ρ v 2 + ρ g h = c o n s t ( 2 . 1 . 2 )
考虑到水为不可压缩的连续流体,因此可以应用伯努利定理得到以下约束方程。v 0 v_0 v 0 v v v h h h r 0 r_0 r 0 S S S
根据自由落体可得p = 0 p=0 p = 0
∫ v d S = v S = c o n s t = v 0 S 0 (2.1.3) ∫vdS=vS=const=v_0 S_0\tag{2.1.3}
∫ v d S = v S = c o n s t = v 0 S 0 ( 2 . 1 . 3 )
0.5 ρ v 2 + ρ g h = c o n s t = 0.5 ρ v 0 2 (2.1.4) 0.5ρv^2+ρgh=const=0.5ρv_0^2\tag{2.1.4}
0 . 5 ρ v 2 + ρ g h = c o n s t = 0 . 5 ρ v 0 2 ( 2 . 1 . 4 )
联立可得
S = S 0 v 0 2 v 0 2 + 2 g h (2.1.5) S=S_0\sqrt{\frac{v_0^2}{v_0^2+2gh}}\tag{2.1.5}
S = S 0 v 0 2 + 2 g h v 0 2 ( 2 . 1 . 5 )
r = r 0 v 0 2 v 0 2 + 2 g h 4 (2.1.6) r=r_0\sqrt[4]{\frac{v_0^2}{v_0^2+2gh}}\tag{2.1.6}
r = r 0 4 v 0 2 + 2 g h v 0 2 ( 2 . 1 . 6 )
该式为下落高度与半径的关系。
2.2. 基于纳维-斯托克斯方程的计算
2.2.1. 连续性方程
在这里我们考虑一个半径为R 0 R_0 R 0 ρ ρ ρ σ σ σ
∂ ρ ∂ t + ∇ ρ v = 0 {\frac{∂ρ}{∂t}}+∇ρv=0
∂ t ∂ ρ + ∇ ρ v = 0
∂ ρ ∂ t = 0 {\frac{∂ρ}{∂t}}=0
∂ t ∂ ρ = 0
图3
为了得到振动方程,我们假设水流柱的半径在进行微小的震动。其振幅为α α α α ≪ R 0 α≪R_0 α ≪ R 0 ω ω ω
R ~ = R 0 + α e i ( ω t + k x ) (2.2.1) \widetilde{R}=R_0+αe^{i(ωt+kx)}\tag{2.2.1}
R = R 0 + α e i ( ω t + k x ) ( 2 . 2 . 1 )
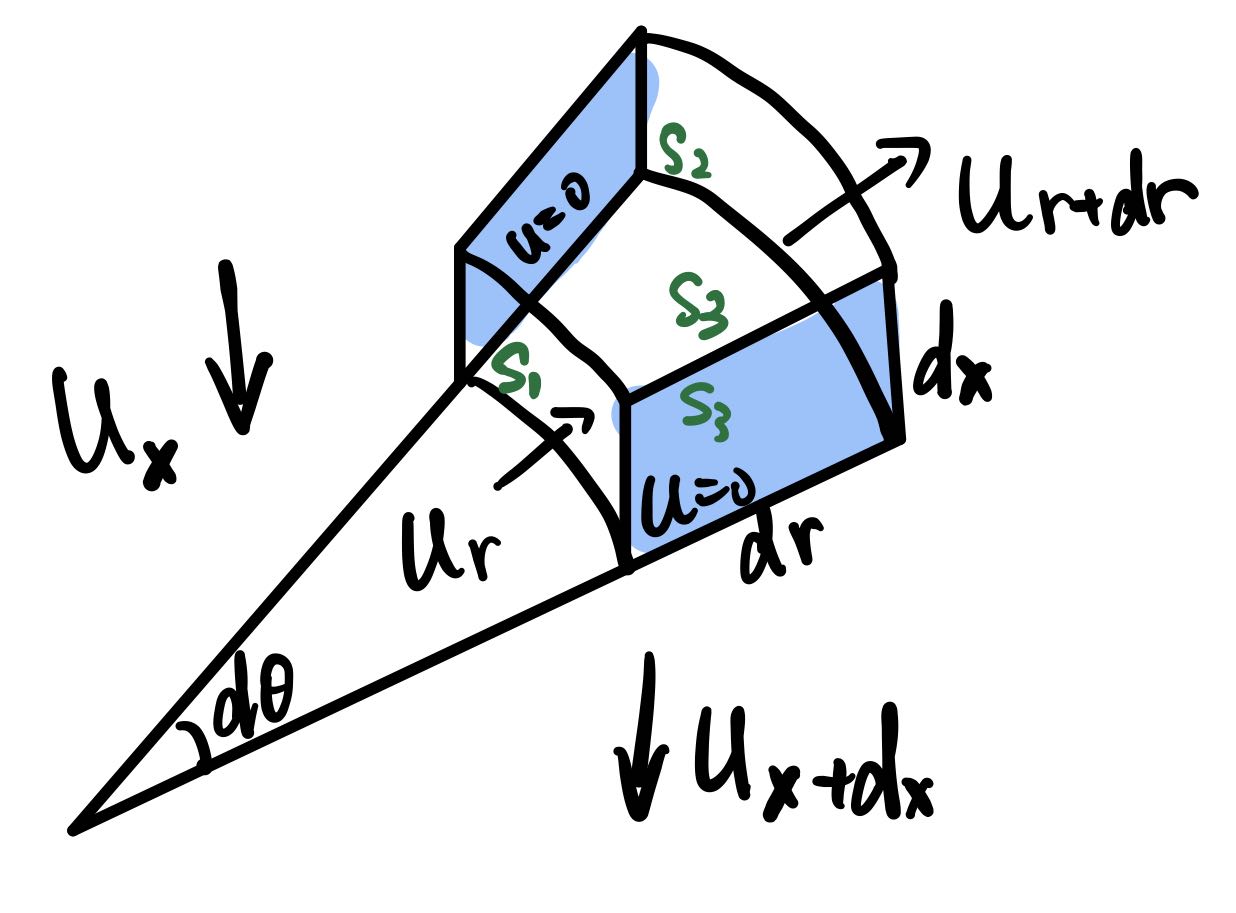
u r S 2 + u x S 3 − u x + d x S 3 = 0 u_r S_2+u_x S_3-u_{x+dx} S_3=0
u r S 2 + u x S 3 − u x + d x S 3 = 0
u r r d θ d x − u r + d r ( r + d r ) d θ d x + ( u x − u x + d x ) ( 1 2 ( r + d r ) 2 − 1 2 r 2 ) d θ = 0 u_rrdθdx-u_{r+dr} (r+dr)dθdx+(u_x-u_{x+dx})(\frac{1}{2}(r+dr)^2-\frac{1}{2}r^2)dθ=0
u r r d θ d x − u r + d r ( r + d r ) d θ d x + ( u x − u x + d x ) ( 2 1 ( r + d r ) 2 − 2 1 r 2 ) d θ = 0
将( 1 2 ( r + d r ) 2 − 1 2 r 2 ) (\frac{1}{2}(r+dr)^2-\frac{1}{2}r^2) ( 2 1 ( r + d r ) 2 − 2 1 r 2 )
1 2 ( r + d r ) 2 − 1 2 r 2 ≈ r d r ( d r r → 0 ) \frac{1}{2}(r+dr)^2-\frac{1}{2}r^2≈rdr\space\space(\frac{dr}{r}→0)
2 1 ( r + d r ) 2 − 2 1 r 2 ≈ r d r ( r d r → 0 )
u r + d r − u r d r r + u r + d r + u x + d x − u x d x r = 0 (2.2.2) \frac{u_{r+dr}-u_r}{dr} r+u_{r+dr}+\frac{u_{x+dx}-u_x}{dx} r=0\tag{2.2.2}
d r u r + d r − u r r + u r + d r + d x u x + d x − u x r = 0 ( 2 . 2 . 2 )
此处u r + d r − u r u_{r+dr}-u_r u r + d r − u r u x + d x − u x u_{x+dx}-u_x u x + d x − u x r r r
2.2.2. 纳维-斯托克斯方程
根据非粘性流体的纳维-斯托克斯方程可以得到
∂ ρ v ∂ t + ∇ ( ρ v ⋅ v ) = ∇ p + ρ g \frac{∂ρ\textbf{\textit{v}}}{∂t}+∇(ρ\textbf{\textit{v}}\cdot\textbf{\textit{v}})=∇\textbf{\textit{p}}+ρg
∂ t ∂ ρ v + ∇ ( ρ v ⋅ v ) = ∇ p + ρ g
此外由于水的不可压缩性质
∂ v ∂ t + ∇ ( v ⋅ v ) = ∇ p ρ (2.2.3) \frac{∂\textbf{\textit{v}}}{∂t}+∇(\textbf{\textit{v}}\cdot\textbf{\textit{v}})=\frac{∇\textbf{\textit{p}}}{ρ}\tag{2.2.3}
∂ t ∂ v + ∇ ( v ⋅ v ) = ρ ∇ p ( 2 . 2 . 3 )
将纳维-斯托克斯方程应用到非粘性流体。并使θ θ θ
∂ u θ ∂ t = 0 \frac{∂u_θ}{∂t}=0
∂ t ∂ u θ = 0
{ ∂ u r ∂ t + u r ∂ u r ∂ r + u x ∂ u r ∂ x = − 1 ρ ∂ p ∂ r ∂ u x ∂ t + u r ∂ u x ∂ r + u x ∂ u x ∂ x = − 1 ρ ∂ p ∂ x (2.2.4) \begin{cases}
\frac{∂u_r}{∂t}+u_r\frac{∂u_r}{∂r}+u_x\frac{∂u_r}{∂x} =-\frac{1}{ρ}\frac{∂p}{∂r}\\
\frac{∂u_x}{∂t}+u_r\frac{∂u_x}{∂r}+u_x\frac{∂u_x}{∂x}=-\frac{1}{ρ}\frac{∂p}{∂x}\\
\end{cases}\tag{2.2.4} { ∂ t ∂ u r + u r ∂ r ∂ u r + u x ∂ x ∂ u r = − ρ 1 ∂ r ∂ p ∂ t ∂ u x + u r ∂ r ∂ u x + u x ∂ x ∂ u x = − ρ 1 ∂ x ∂ p ( 2 . 2 . 4 )
将上式含有高阶α α α
{ ∂ u r ∂ t = − 1 ρ ∂ p ∂ r ∂ u x ∂ t = − 1 ρ ∂ p ∂ x (2.2.5) \begin{cases}
\frac{∂u_r}{∂t}=-\frac{1}{ρ}\frac{∂p}{∂r}\\
\frac{∂u_x}{∂t}=-\frac{1}{ρ}\frac{∂p}{∂x}\\
\end{cases}\tag{2.2.5} { ∂ t ∂ u r = − ρ 1 ∂ r ∂ p ∂ t ∂ u x = − ρ 1 ∂ x ∂ p ( 2 . 2 . 5 )
此处将速度与压力表示为和R R R
{ R ~ = R 0 + α e i ( ω t + k x ) u r = R ( r ) α e i ( ω t + k x ) u x = X ( r ) α e i ( ω t + k x ) p = P ( r ) e i ( ω t + k x ) (2.2.6) \begin{cases}
\widetilde{R}=R_0+\alpha e^{i(\omega t+kx)}\\
u_r=R(r)\alpha e^{i(\omega t+kx)}\\
u_x=X(r)\alpha e^{i(\omega t+kx)}\\
p=P(r)e^{i(\omega t+kx)}\\
\end{cases}\tag{2.2.6} ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ R = R 0 + α e i ( ω t + k x ) u r = R ( r ) α e i ( ω t + k x ) u x = X ( r ) α e i ( ω t + k x ) p = P ( r ) e i ( ω t + k x ) ( 2 . 2 . 6 )
2.2.3. 振动方程及其解析解
将式(2.2.6)和式(2.2.5)带入到式(2.2.2)。
{ − 1 ρ ∂ p ∂ r = i ω R − 1 ρ i p k = i ω X d R d r + R r + i k X = 0 (2.2.7) \begin{cases}
-\frac{1}{ρ}\frac{∂p}{∂r}=i\omega R\\
-\frac{1}{ρ}ipk=i\omega X\\
\frac{dR}{dr}+\frac{R}{r}+ikX=0\\
\end{cases}\tag{2.2.7}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ − ρ 1 ∂ r ∂ p = i ω R − ρ 1 i p k = i ω X d r d R + r R + i k X = 0 ( 2 . 2 . 7 )
将式(2.2.7)中的式2与式3分别关于X X X R R R
{ − 1 ρ ∂ p ∂ r = i ω R − 1 ρ i k ∂ p ∂ r = i ω d X d r d 2 R d r 2 − R r 2 + 1 r d R d r + i k d X d r = 0 (2.2.8) \begin{cases}
-\frac{1}{ρ}\frac{∂p}{∂r}=i\omega R\\
-\frac{1}{ρ}ik\frac{∂p}{∂r}=i\omega \frac{dX}{dr}\\
\frac{d^2R}{dr^2}-\frac{R}{r^2}+\frac{1}{r}\frac{dR}{dr}+ik\frac{dX}{dr}=0\\
\end{cases}\tag{2.2.8}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ − ρ 1 ∂ r ∂ p = i ω R − ρ 1 i k ∂ r ∂ p = i ω d r d X d r 2 d 2 R − r 2 R + r 1 d r d R + i k d r d X = 0 ( 2 . 2 . 8 )
联立后可以得到以下方程
r 2 d 2 R d r 2 + r d R d r − R ( 1 + k 2 r 2 ) = 0 (2.2.9) r^2\frac{d^2R}{dr^2}+r\frac{dR}{dr}-R(1+k^2 r^2)=0\tag{2.2.9}
r 2 d r 2 d 2 R + r d r d R − R ( 1 + k 2 r 2 ) = 0 ( 2 . 2 . 9 )
此微分方程的一次修正贝塞尔方程,其解可以使用第一种修正贝塞尔函数进行表示。
R ( r ) = C 1 I 1 ( k r ) (2.2.10) R(r)=C_1 I_1 (kr)\tag{2.2.10}
R ( r ) = C 1 I 1 ( k r ) ( 2 . 2 . 1 0 )
接下来将该解带入边界条件。
边界条件1:圆柱半径的变化率
考虑液体柱的一个截面,在r = R 0 r=R_0 r = R 0 u r = d R d t u_r=\frac{dR}{dt} u r = d t d R
u r = R ( R 0 ) α e i ( ω t + k x ) = i α ω e i ( ω t + k x ) u_r=R(R_0)αe^{i(ωt+kx)}= iαωe^{i(ωt+kx)}
u r = R ( R 0 ) α e i ( ω t + k x ) = i α ω e i ( ω t + k x )
R ( R 0 ) = C 1 I 1 ( k R 0 ) = i α ω R(R_0 )=C_1 I_1 (kR_0 )=iαω
R ( R 0 ) = C 1 I 1 ( k R 0 ) = i α ω
C 1 = i α ω I 1 ( k R 0 ) C_1=\frac{iαω}{I_1 (kR_0)}
C 1 = I 1 ( k R 0 ) i α ω
R ( r ) = i α ω I 1 ( k R 0 ) I 1 ( k r ) (2.2.11) R(r)=\frac{iαω}{I_1 (kR_0)}I_1(kr)\tag{2.2.11}
R ( r ) = I 1 ( k R 0 ) i α ω I 1 ( k r ) ( 2 . 2 . 1 1 )
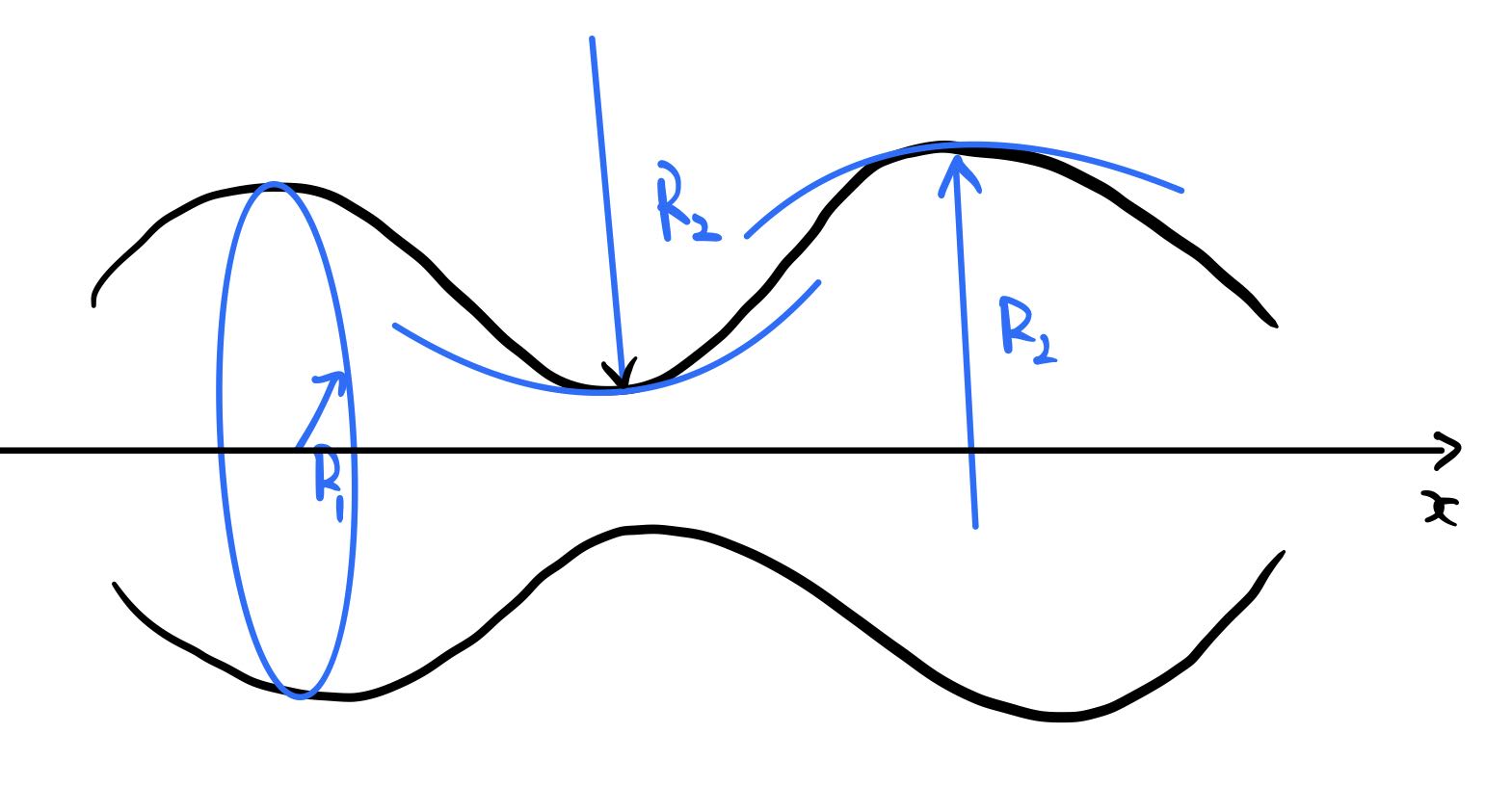
边界条件2:表面张力对圆柱表面的应力
图4
此处P 0 P_0 P 0 p p p
P 0 + p = σ ( 1 R 1 + 1 R 2 ) P_0+p=σ(\frac{1}{R_1}+\frac{1}{R_2})
P 0 + p = σ ( R 1 1 + R 2 1 )
{ P 0 = σ R 0 1 R 1 = c o s θ R 0 + α e i ( ω t + k x ) ≈ 1 R 0 ( 1 − α R 0 e i ( ω t + k x ) ) 1 R 2 = − ∂ 2 R ∂ x 2 = α k 2 e i ( ω t + k x ) \begin{cases}
P_0=\frac{σ}{R_0} \\
\frac{1}{R_1} =\frac{cosθ}{R_0+αe^{i(ωt+kx)}}≈\frac{1}{R_0} (1-\frac{α}{R_0} e^{i(ωt+kx)} )\\
\frac{1}{R_2} =-\frac{∂^2R}{∂x^2}=αk^2 e^{i(ωt+kx)} \\
\end{cases}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ P 0 = R 0 σ R 1 1 = R 0 + α e i ( ω t + k x ) c o s θ ≈ R 0 1 ( 1 − R 0 α e i ( ω t + k x ) ) R 2 1 = − ∂ x 2 ∂ 2 R = α k 2 e i ( ω t + k x )
1 R 1 \frac{1}{R_1} R 1 1 c o s θ cosθ c o s θ c o s θ = 1 + o ( α 2 ) cosθ=1+o(α^2) c o s θ = 1 + o ( α 2 )
联立可得如下方程。
p = σ ( 1 R 1 + 1 R 2 ) − P 0 = α σ R 0 2 ( k 2 R 0 2 − 1 ) e i ( ω t + k x ) p=σ(\frac{1}{R_1} +\frac{1}{R_2})-P_0=\frac{ασ}{R_0^2} (k^2 R_0^2-1) e^{i(ωt+kx)}
p = σ ( R 1 1 + R 2 1 ) − P 0 = R 0 2 α σ ( k 2 R 0 2 − 1 ) e i ( ω t + k x )
接下来将解得的微分方程式代入式(2.2.7)− 1 ρ ∂ p ∂ r = i ω R -\frac{1}{ρ}\frac{∂p}{∂r}=iωR − ρ 1 ∂ r ∂ p = i ω R P ( r ) P(r) P ( r )
P ( r ) = − i ⋅ i α ρ ω 2 I 1 ( k R 0 ) ∫ I 1 ( k r ) d r P(r)=-\frac{i\cdot iαρω^2}{I_1 (kR_0)}∫{I_1 (kr)dr}
P ( r ) = − I 1 ( k R 0 ) i ⋅ i α ρ ω 2 ∫ I 1 ( k r ) d r
= α ρ ω 2 I 1 ( k R 0 ) ∫ 0 r I 1 ( k r ) d r =\frac{αρω^2}{I_1 (kR_0)} \int_0^{r}{I_1 (kr)dr}
= I 1 ( k R 0 ) α ρ ω 2 ∫ 0 r I 1 ( k r ) d r
= α ρ ω 2 k I 0 ( k r ) I 1 ( k R 0 ) (2.2.12) =\frac{αρω^2}{k}\frac{I_0 (kr)}{I_1(kR_0)}\tag{2.2.12}
= k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k r ) ( 2 . 2 . 1 2 )
由此可得,
p = α ρ ω 2 k I 0 ( k r ) I 1 ( k R 0 ) e i ( ω t + k x ) (2.2.13) p=\frac{αρω^2}{k}\frac{I_0 (kr)}{I_1(kR_0)}e^{i(ωt+kx)}\tag{2.2.13}
p = k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k r ) e i ( ω t + k x ) ( 2 . 2 . 1 3 )
将计算边界条件时得到的关于p p p p p p
α σ R 0 2 ( k 2 R 2 − 1 ) = α ρ ω 2 k I 0 ( k R 0 ) I 1 ( k R 0 ) \frac{ασ}{R_0^2}(k^2R^2-1)=\frac{αρω^2}{k}\frac{I_0 (kR_0)}{I_1(kR_0)}
R 0 2 α σ ( k 2 R 2 − 1 ) = k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k R 0 )
由此可得ω ω ω R 0 k R_0 k R 0 k
ω 2 = σ ρ R 0 3 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) (2.2.14) ω^2=\frac{σ}{ρR_0^3}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\tag{2.2.14}
ω 2 = ρ R 0 3 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) ( 2 . 2 . 1 4 )
液体的下落速度与圆柱液体的振动向上传播的速度相同的时候,液体柱的振动就会就表现为驻波的形态。
也就是v = ω k v=\frac{ω}{k} v = k ω
v 2 = ω 2 k 2 = σ ρ k R 0 2 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) (2.2.15) v^2=\frac{ω^2}{k^2}=\frac{σ}{ρkR_0^2}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\tag{2.2.15}
v 2 = k 2 ω 2 = ρ k R 0 2 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) ( 2 . 2 . 1 5 )
此外,由于微小振动的波长为λ = 2 π k = 2 π R 0 k R 0 λ=\frac{2π}{k}=\frac{2πR_0}{kR_0} λ = k 2 π = k R 0 2 π R 0
{ v 2 = ω 2 k 2 = σ ρ k R 0 2 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) λ = 2 π k = 2 π R 0 k R 0 (2.2.16) \begin{cases}
v^2=\frac{ω^2}{k^2}=\frac{σ}{ρkR_0^2}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\\
λ=\frac{2π}{k}=\frac{2πR_0}{kR_0}\\
\end{cases}\tag{2.2.16}
{ v 2 = k 2 ω 2 = ρ k R 0 2 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) λ = k 2 π = k R 0 2 π R 0 ( 2 . 2 . 1 6 )
2.2.4. 数值计算
接下来使用Python绘制式(2.2.15)的图像,修正贝塞尔函数可以通过scipy.special来进行计算。
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) f(kR_0)=kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 )
Python代码如下
from scipy import special
import numpy as np
import matplotlib.pyplot as plt
x = []
y = []
for i in range(100000):
xi=i / 100000
IV1=special.iv(1,xi)
IV0=special.iv(0,xi)
y.append(IV1/IV0 * (1 - xi**2) * xi)
x.append(xi)
plt.plot(x,y)
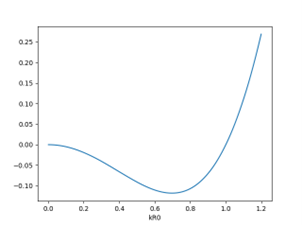
执行上述代码,可以得到f ( k R 0 ) f(kR_0) f ( k R 0 )
図5
当ω 2 ω^2 ω 2 R ~ \widetilde{R} R
R ~ = R 0 + α e − β t + i k x \widetilde{R}=R_0+αe^{-βt+ikx}
R = R 0 + α e − β t + i k x
β = ∣ ω 2 ∣ β=|ω^2 |
β = ∣ ω 2 ∣
因此,此时R ~ \widetilde{R} R k R 0 = 0.697 kR_0=0.697 k R 0 = 0 . 6 9 7
接下来分析ω 2 > 0 ω^2>0 ω 2 > 0
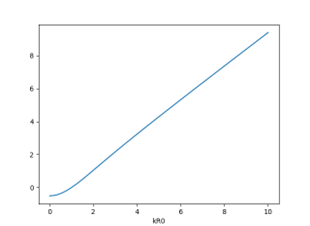
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) f(kR_0)=kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 )
図6
观察图6我们可以发现,该函数曲线在k R 0 kR_0 k R 0 y = x y=x y = x k R 0 kR_0 k R 0
λ = 2 π k = 2 π σ ρ v 2 (2.2.18) λ=\frac{2π}{k}=\frac{2πσ}{ρv^2}\tag{2.2.18}
λ = k 2 π = ρ v 2 2 π σ ( 2 . 2 . 1 8 )
3. 实验
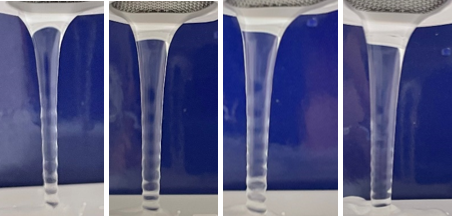
図7
图7为不同流量的液体在同一高度下落时的实验照片(高度约为5cm),由于液体从相同的高度落下,所以在接近接触面处的流速相同。观察实验图可以看出,液体表面微小振动的波长与流量、截面半径无关。
接下来将实验数据带入式(2.2.18)进行验证
v 2 = 2 g h v^2=2gh
v 2 = 2 g h
λ = 2 π σ ρ v 2 λ=\frac{2πσ}{ρv^2}
λ = ρ v 2 2 π σ
因此可得λ = π σ ρ g h = 0.46 m m λ=\frac{πσ}{ρgh}=0.46mm λ = ρ g h π σ = 0 . 4 6 m m
4. 总结
本次研究建模分析了自由下落流体柱的表面振动现象,并尝试计算了液柱振动波长的表达式。通过使用Python进行数值计算,结论如下
解析解:式(2.2.17) ,近似解:式(2.2.18) .
虽然本次研究仅对从水龙头下落的水流柱进行了分析,但该现象广泛存在于各种流体之中。该现象产生机制为液体的表面张力与液体自身的动量,因此只要存在以上两个参数的流体均会产生类似的现象。但本次研究中仅针对非粘滞性流体进行了计算,在分析油性物质等粘滞性流体时还需要对方程进行改动另行分析。
参考文献
[1] Wada, Yoshimasa. On the Steady Surface Ripples of a Cylindrical Flow. Journal of the Physical Society of Japan, 5(4), 259–262, (1950). doi:10.1143/jpsj.5.259
[2] Rayleigh, L. On The Instability Of Jets. Proceedings of the London Mathematical Society, s1 10(1), 4–13, (1878). doi:10.1112/plms/s1-10.




Comment