中文/CN:https://www.cyberwei.com/archives/220810cn
1. 研究背景
図1
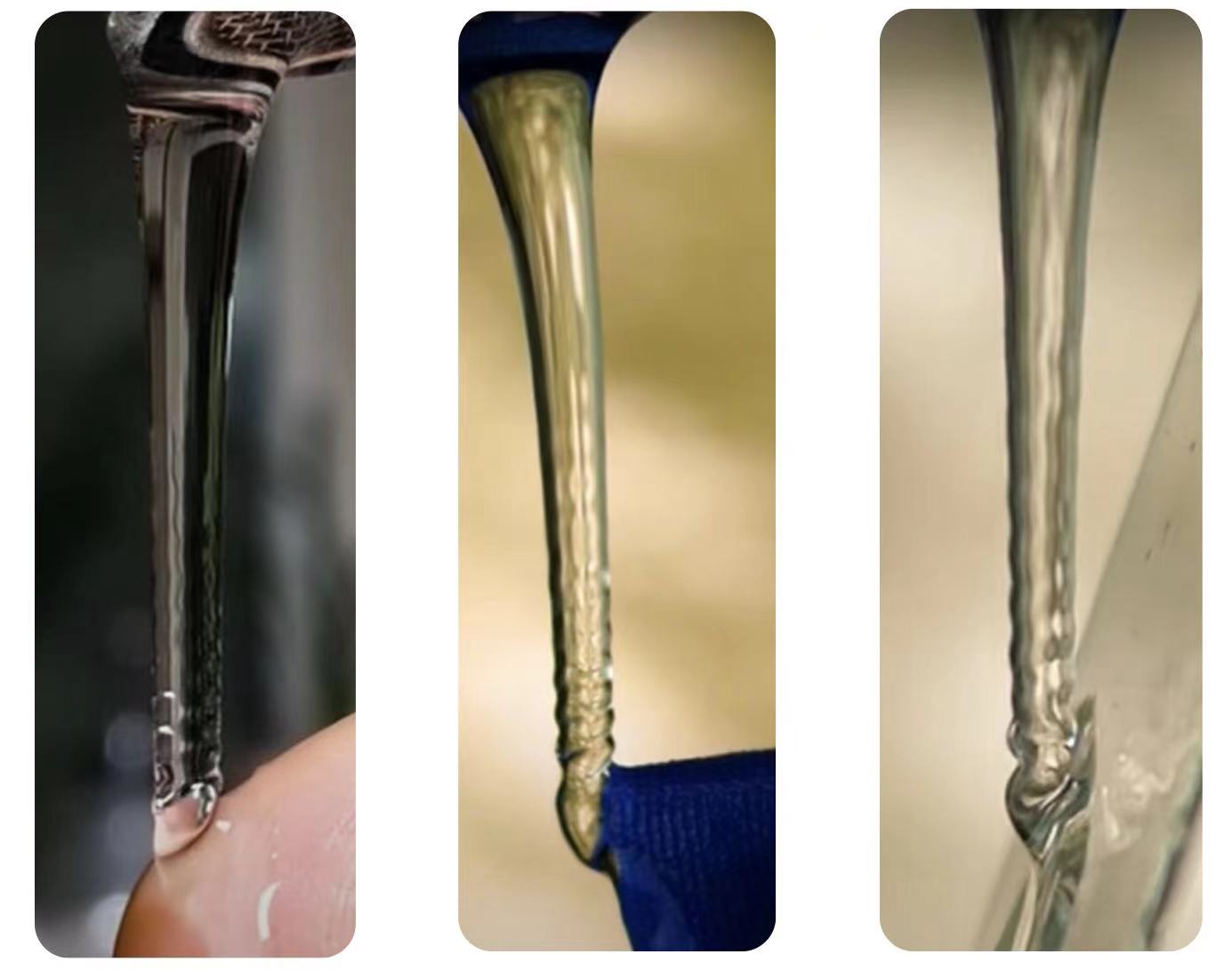
蛇口から出る水流を小さく調整して観察すると,その水流は重力の影響を受けて自由落下していることがわかる.水流の断面は円になっており,落下すると同時にその円半径が縮まっている.十分高い場所から落下させると最終的に水流は千切れ,粒状の水滴になる.また,水流が千切れる前に障害物などに当たると,水流は粒状の水滴にならず,直接障害物の表面に沿って流れる.観察してみると,障害物と衝突する直前の水流の部分が小さな波状の凸凹が生じていることがわかる.その凸凹が生成している同時に,水流量を小さく調整すると,凸凹の細いところから水流が千切れ.つまり,この現象は水流が水滴になる時の原因と同じと推定できる.今回の研究では,この凸凹現象の生成についてのモデリング・計算を行う.
2. 現象のモデリング・計算
図1の波動は定常波のように見られるので,液体の落下速度と液体柱の波動速度の和がゼロと考えられる。そのため,液体柱の波動を計算する必要がある.この論文では流体力学の連続方程式及びナビエストークス方程式を使い計算を行う.
2.1. 自由落下水流の半径変化
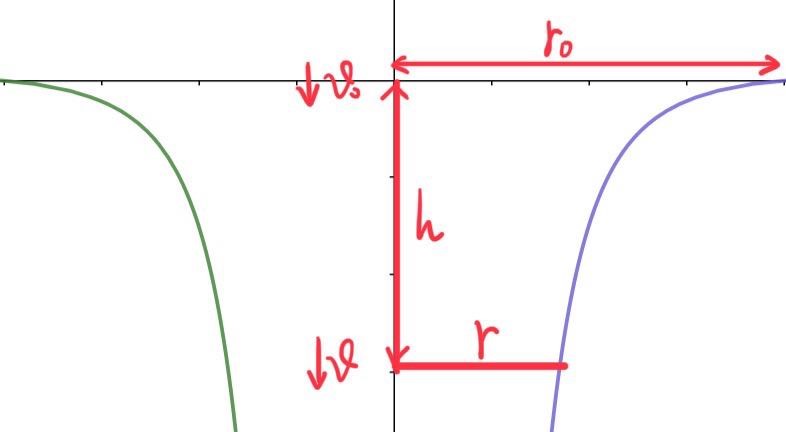
液体柱振動の計算を行う前にまずは自由落下水流の落下高度と断面半径の関係を計算する.
図2
v d S = c o n s t (2.1.1) vdS=const\tag{2.1.1}
v d S = c o n s t ( 2 . 1 . 1 )
p + 0.5 ρ v 2 + ρ g h = c o n s t (2.1.2) p+0.5ρv^2+ρgh=const\tag{2.1.2}
p + 0 . 5 ρ v 2 + ρ g h = c o n s t ( 2 . 1 . 2 )
水は非圧縮性の連続流体で,ベルヌーイの定理により以下の方程式が得られる.v 0 v_0 v 0 v v v h h h r 0 r_0 r 0 S S S
水流は自由落下なのでp = 0 p=0 p = 0
∫ v d S = v S = c o n s t = v 0 S 0 (2.1.3) ∫vdS=vS=const=v_0 S_0\tag{2.1.3}
∫ v d S = v S = c o n s t = v 0 S 0 ( 2 . 1 . 3 )
0.5 ρ v 2 + ρ g h = c o n s t = 0.5 ρ v 0 2 (2.1.4) 0.5ρv^2+ρgh=const=0.5ρv_0^2\tag{2.1.4}
0 . 5 ρ v 2 + ρ g h = c o n s t = 0 . 5 ρ v 0 2 ( 2 . 1 . 4 )
連立すると
S = S 0 v 0 2 v 0 2 + 2 g h (2.1.5) S=S_0\sqrt{\frac{v_0^2}{v_0^2+2gh}}\tag{2.1.5}
S = S 0 v 0 2 + 2 g h v 0 2 ( 2 . 1 . 5 )
r = r 0 v 0 2 v 0 2 + 2 g h 4 (2.1.6) r=r_0\sqrt[4]{\frac{v_0^2}{v_0^2+2gh}}\tag{2.1.6}
r = r 0 4 v 0 2 + 2 g h v 0 2 ( 2 . 1 . 6 )
落下高度と半径の関係がわかる.
2.2. ナビエストークス方程式を基づいた計算
2.2.1. 連続性方程式
ここでは半径R 0 R_0 R 0 ρ ρ ρ σ σ σ
∂ ρ ∂ t + ∇ ρ v = 0 {\frac{∂ρ}{∂t}}+∇ρv=0
∂ t ∂ ρ + ∇ ρ v = 0
∂ ρ ∂ t = 0 {\frac{∂ρ}{∂t}}=0
∂ t ∂ ρ = 0
図3
振動を分析するために,この円柱の液体の表面が微小な摂動をしていると考える.ここではα ≪ R 0 α≪R_0 α ≪ R 0
R ~ = R 0 + α e i ( ω t + k x ) (2.2.1) \widetilde{R}=R_0+αe^{i(ωt+kx)}\tag{2.2.1}
R = R 0 + α e i ( ω t + k x ) ( 2 . 2 . 1 )
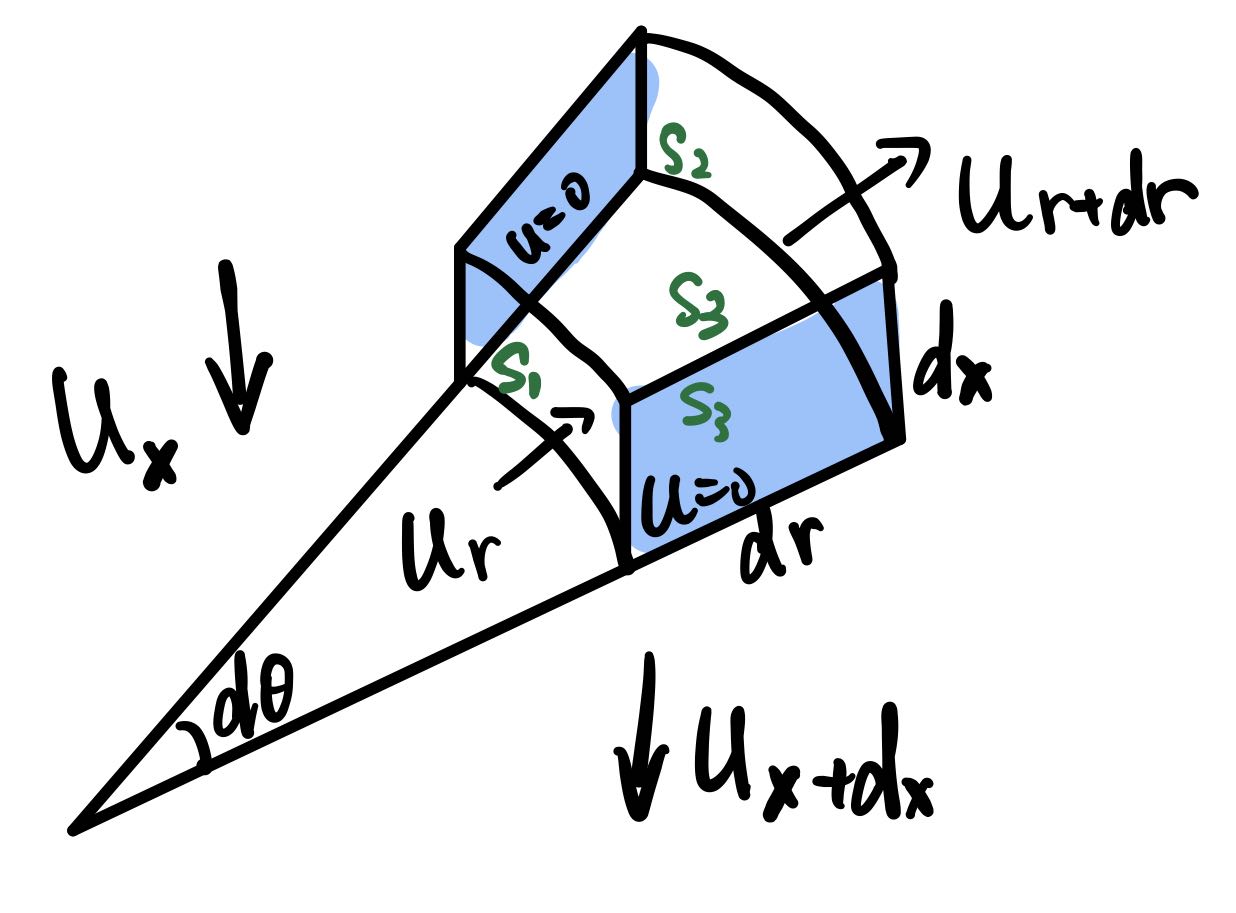
u r S 2 + u x S 3 − u x + d x S 3 = 0 u_r S_2+u_x S_3-u_{x+dx} S_3=0
u r S 2 + u x S 3 − u x + d x S 3 = 0
u r r d θ d x − u r + d r ( r + d r ) d θ d x + ( u x − u x + d x ) ( 1 2 ( r + d r ) 2 − 1 2 r 2 ) d θ = 0 u_rrdθdx-u_{r+dr} (r+dr)dθdx+(u_x-u_{x+dx})(\frac{1}{2}(r+dr)^2-\frac{1}{2}r^2)dθ=0
u r r d θ d x − u r + d r ( r + d r ) d θ d x + ( u x − u x + d x ) ( 2 1 ( r + d r ) 2 − 2 1 r 2 ) d θ = 0
( 1 2 ( r + d r ) 2 − 1 2 r 2 ) (\frac{1}{2}(r+dr)^2-\frac{1}{2}r^2) ( 2 1 ( r + d r ) 2 − 2 1 r 2 )
1 2 ( r + d r ) 2 − 1 2 r 2 ≈ r d r ( d r r → 0 ) \frac{1}{2}(r+dr)^2-\frac{1}{2}r^2≈rdr\space\space(\frac{dr}{r}→0)
2 1 ( r + d r ) 2 − 2 1 r 2 ≈ r d r ( r d r → 0 )
u ( r + d r ) − u r d r r + u r + d r + u ( x + d x ) − u x d x r = 0 (2.2.2) \frac{u_(r+dr)-u_r}{dr} r+u_{r+dr}+\frac{u_(x+dx)-u_x}{dx} r=0\tag{2.2.2}
d r u ( r + d r ) − u r r + u r + d r + d x u ( x + d x ) − u x r = 0 ( 2 . 2 . 2 )
u r + d r − u r u_{r+dr}-u_r u r + d r − u r u x + d x − u x u_{x+dx}-u_x u x + d x − u x
2.2.2. ナビエストークス方程式
次は非粘性流体のナビエストークス方程式を使って計算する.
∂ ρ v ∂ t + ∇ ( ρ v ⋅ v ) = ∇ p + ρ g \frac{∂ρ\textbf{\textit{v}}}{∂t}+∇(ρ\textbf{\textit{v}}\cdot\textbf{\textit{v}})=∇\textbf{\textit{p}}+ρg
∂ t ∂ ρ v + ∇ ( ρ v ⋅ v ) = ∇ p + ρ g
今回分析する流体は非圧縮性流体なので,以下の式が得られる.
∂ v ∂ t + ∇ ( v ⋅ v ) = ∇ p ρ (2.2.3) \frac{∂\textbf{\textit{v}}}{∂t}+∇(\textbf{\textit{v}}\cdot\textbf{\textit{v}})=\frac{∇\textbf{\textit{p}}}{ρ}\tag{2.2.3}
∂ t ∂ v + ∇ ( v ⋅ v ) = ρ ∇ p ( 2 . 2 . 3 )
円柱座標でのナビエストークス方程式は以下の形式になる.θ θ θ
∂ u θ ∂ t = 0 \frac{∂u_θ}{∂t}=0
∂ t ∂ u θ = 0
{ ∂ u r ∂ t + u r ∂ u r ∂ r + u x ∂ u r ∂ x = − 1 ρ ∂ p ∂ r ∂ u x ∂ t + u r ∂ u x ∂ r + u x ∂ u x ∂ x = − 1 ρ ∂ p ∂ x (2.2.4) \begin{cases}
\frac{∂u_r}{∂t}+u_r\frac{∂u_r}{∂r}+u_x\frac{∂u_r}{∂x} =-\frac{1}{ρ}\frac{∂p}{∂r}\\
\frac{∂u_x}{∂t}+u_r\frac{∂u_x}{∂r}+u_x\frac{∂u_x}{∂x}=-\frac{1}{ρ}\frac{∂p}{∂x}\\
\end{cases}\tag{2.2.4} { ∂ t ∂ u r + u r ∂ r ∂ u r + u x ∂ x ∂ u r = − ρ 1 ∂ r ∂ p ∂ t ∂ u x + u r ∂ r ∂ u x + u x ∂ x ∂ u x = − ρ 1 ∂ x ∂ p ( 2 . 2 . 4 )
上記の式は微小振幅α α α
{ ∂ u r ∂ t = − 1 ρ ∂ p ∂ r ∂ u x ∂ t = − 1 ρ ∂ p ∂ x (2.2.5) \begin{cases}
\frac{∂u_r}{∂t}=-\frac{1}{ρ}\frac{∂p}{∂r}\\
\frac{∂u_x}{∂t}=-\frac{1}{ρ}\frac{∂p}{∂x}\\
\end{cases}\tag{2.2.5} { ∂ t ∂ u r = − ρ 1 ∂ r ∂ p ∂ t ∂ u x = − ρ 1 ∂ x ∂ p ( 2 . 2 . 5 )
ここでは速度と圧力の摂動をR R R
{ R ~ = R 0 + α e i ( ω t + k x ) u r = R ( r ) α e i ( ω t + k x ) u x = X ( r ) α e i ( ω t + k x ) p = P ( r ) e i ( ω t + k x ) (2.2.6) \begin{cases}
\widetilde{R}=R_0+\alpha e^{i(\omega t+kx)}\\
u_r=R(r)\alpha e^{i(\omega t+kx)}\\
u_x=X(r)\alpha e^{i(\omega t+kx)}\\
p=P(r)e^{i(\omega t+kx)}\\
\end{cases}\tag{2.2.6} ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ R = R 0 + α e i ( ω t + k x ) u r = R ( r ) α e i ( ω t + k x ) u x = X ( r ) α e i ( ω t + k x ) p = P ( r ) e i ( ω t + k x ) ( 2 . 2 . 6 )
2.2.3. 振動方程式の導出及びその解
式(2.2.6)を(2.2.5)と(2.2.2)に代入する.
{ − 1 ρ ∂ p ∂ r = i ω R − 1 ρ i p k = i ω X d R d r + R r + i k X = 0 (2.2.7) \begin{cases}
-\frac{1}{ρ}\frac{∂p}{∂r}=i\omega R\\
-\frac{1}{ρ}ipk=i\omega X\\
\frac{dR}{dr}+\frac{R}{r}+ikX=0\\
\end{cases}\tag{2.2.7}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ − ρ 1 ∂ r ∂ p = i ω R − ρ 1 i p k = i ω X d r d R + r R + i k X = 0 ( 2 . 2 . 7 )
式(2.2.7)の式2と式3をそれぞれXとRに対して微分する.
{ − 1 ρ ∂ p ∂ r = i ω R − 1 ρ i k ∂ p ∂ r = i ω d X d r d 2 R d r 2 − R r 2 + 1 r d R d r + i k d X d r = 0 (2.2.8) \begin{cases}
-\frac{1}{ρ}\frac{∂p}{∂r}=i\omega R\\
-\frac{1}{ρ}ik\frac{∂p}{∂r}=i\omega \frac{dX}{dr}\\
\frac{d^2R}{dr^2}-\frac{R}{r^2}+\frac{1}{r}\frac{dR}{dr}+ik\frac{dX}{dr}=0\\
\end{cases}\tag{2.2.8}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ − ρ 1 ∂ r ∂ p = i ω R − ρ 1 i k ∂ r ∂ p = i ω d r d X d r 2 d 2 R − r 2 R + r 1 d r d R + i k d r d X = 0 ( 2 . 2 . 8 )
上記の式を連立して以下の微分方程式が得られる
r 2 d 2 R d r 2 + r d R d r − R ( 1 + k 2 r 2 ) = 0 (2.2.9) r^2\frac{d^2R}{dr^2}+r\frac{dR}{dr}-R(1+k^2 r^2)=0\tag{2.2.9}
r 2 d r 2 d 2 R + r d r d R − R ( 1 + k 2 r 2 ) = 0 ( 2 . 2 . 9 )
この微分方程式は1次の修正ベッセル関数である.方程式の解は第一種修正ベッセル関数で表すことができる.
R ( r ) = C 1 I 1 ( k r ) (2.2.10) R(r)=C_1 I_1 (kr)\tag{2.2.10}
R ( r ) = C 1 I 1 ( k r ) ( 2 . 2 . 1 0 )
次はこの方程式の境界条件を考える.
境界条件1:円柱自身の半径の変化率
この時,r = R 0 r=R_0 r = R 0 u r = d R d t u_r=\frac{dR}{dt} u r = d t d R
u r = R ( R 0 ) α e i ( ω t + k x ) = i α ω e i ( ω t + k x ) u_r=R(R_0)αe^{i(ωt+kx)}= iαωe^{i(ωt+kx)}
u r = R ( R 0 ) α e i ( ω t + k x ) = i α ω e i ( ω t + k x )
R ( R 0 ) = C 1 I 1 ( k R 0 ) = i α ω R(R_0 )=C_1 I_1 (kR_0 )=iαω
R ( R 0 ) = C 1 I 1 ( k R 0 ) = i α ω
C 1 = i α ω I 1 ( k R 0 ) C_1=\frac{iαω}{I_1 (kR_0)}
C 1 = I 1 ( k R 0 ) i α ω
R ( r ) = i α ω I 1 ( k R 0 ) I 1 ( k r ) (2.2.11) R(r)=\frac{iαω}{I_1 (kR_0)}I_1(kr)\tag{2.2.11}
R ( r ) = I 1 ( k R 0 ) i α ω I 1 ( k r ) ( 2 . 2 . 1 1 )
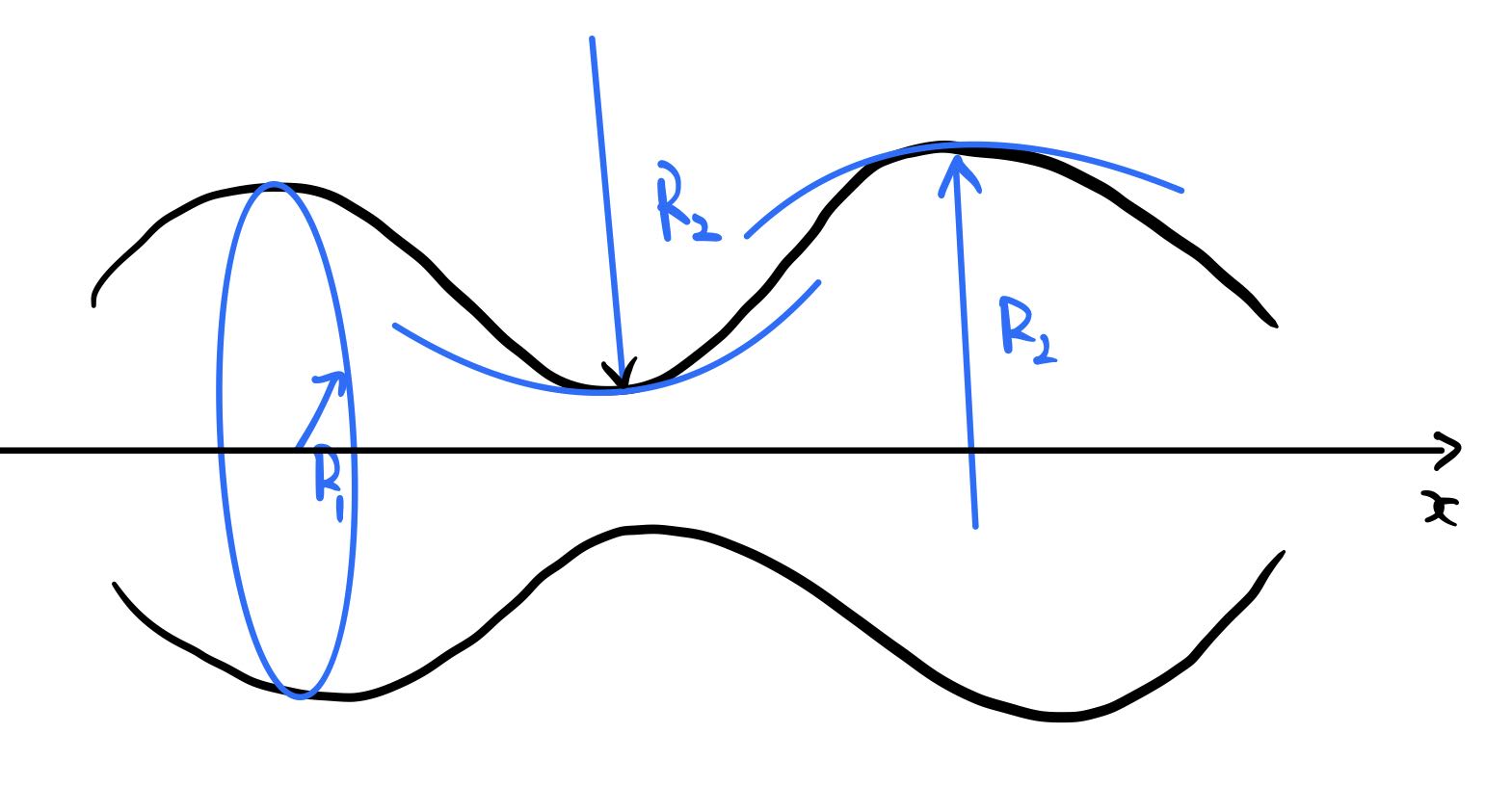
境界条件2:円柱表面の表面張力による応力
図4
P 0 P_0 P 0 p p p
P 0 + p = σ ( 1 R 1 + 1 R 2 ) P_0+p=σ(\frac{1}{R_1}+\frac{1}{R_2})
P 0 + p = σ ( R 1 1 + R 2 1 )
{ P 0 = σ R 0 1 R 1 = c o s θ R 0 + α e i ( ω t + k x ) ≈ 1 R 0 ( 1 − α R 0 e i ( ω t + k x ) ) 1 R 2 = − ∂ 2 R ∂ x 2 = α k 2 e i ( ω t + k x ) \begin{cases}
P_0=\frac{σ}{R_0} \\
\frac{1}{R_1} =\frac{cosθ}{R_0+αe^{i(ωt+kx)}}≈\frac{1}{R_0} (1-\frac{α}{R_0} e^{i(ωt+kx)} )\\
\frac{1}{R_2} =-\frac{∂^2R}{∂x^2}=αk^2 e^{i(ωt+kx)} \\
\end{cases}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ P 0 = R 0 σ R 1 1 = R 0 + α e i ( ω t + k x ) c o s θ ≈ R 0 1 ( 1 − R 0 α e i ( ω t + k x ) ) R 2 1 = − ∂ x 2 ∂ 2 R = α k 2 e i ( ω t + k x )
1 R 1 \frac{1}{R_1} R 1 1 α α α
p = σ ( 1 R 1 + 1 R 2 ) − P 0 = α σ R 0 2 ( k 2 R 0 2 − 1 ) e i ( ω t + k x ) p=σ(\frac{1}{R_1} +\frac{1}{R_2})-P_0=\frac{ασ}{R_0^2} (k^2 R_0^2-1) e^{i(ωt+kx)}
p = σ ( R 1 1 + R 2 1 ) − P 0 = R 0 2 α σ ( k 2 R 0 2 − 1 ) e i ( ω t + k x )
次は解いた微分方程式(2.2.11)を式(2.2.7)− 1 ρ ∂ p ∂ r = i ω R -\frac{1}{ρ}\frac{∂p}{∂r}=iωR − ρ 1 ∂ r ∂ p = i ω R P ( r ) P(r) P ( r )
P ( r ) = − i ⋅ i α ρ ω 2 I 1 ( k R 0 ) ∫ I 1 ( k r ) d r P(r)=-\frac{i\cdot iαρω^2}{I_1 (kR_0)}∫{I_1 (kr)dr}
P ( r ) = − I 1 ( k R 0 ) i ⋅ i α ρ ω 2 ∫ I 1 ( k r ) d r
= α ρ ω 2 I 1 ( k R 0 ) ∫ 0 r I 1 ( k r ) d r =\frac{αρω^2}{I_1 (kR_0)} \int_0^{r}{I_1 (kr)dr}
= I 1 ( k R 0 ) α ρ ω 2 ∫ 0 r I 1 ( k r ) d r
= α ρ ω 2 k I 0 ( k r ) I 1 ( k R 0 ) (2.2.12) =\frac{αρω^2}{k}\frac{I_0 (kr)}{I_1(kR_0)}\tag{2.2.12}
= k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k r ) ( 2 . 2 . 1 2 )
よって,
p = α ρ ω 2 k I 0 ( k r ) I 1 ( k R 0 ) e i ( ω t + k x ) (2.2.13) p=\frac{αρω^2}{k}\frac{I_0 (kr)}{I_1(kR_0)}e^{i(ωt+kx)}\tag{2.2.13}
p = k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k r ) e i ( ω t + k x ) ( 2 . 2 . 1 3 )
境界条件で得たp p p p p p
α σ R 0 2 ( k 2 R 2 − 1 ) = α ρ ω 2 k I 0 ( k R 0 ) I 1 ( k R 0 ) \frac{ασ}{R_0^2}(k^2R^2-1)=\frac{αρω^2}{k}\frac{I_0 (kR_0)}{I_1(kR_0)}
R 0 2 α σ ( k 2 R 2 − 1 ) = k α ρ ω 2 I 1 ( k R 0 ) I 0 ( k R 0 )
ω ω ω R 0 k R_0 k R 0 k
ω 2 = σ ρ R 0 3 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) (2.2.14) ω^2=\frac{σ}{ρR_0^3}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\tag{2.2.14}
ω 2 = ρ R 0 3 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) ( 2 . 2 . 1 4 )
液体の下落の速度と円柱液体の振動が上に遡る速度が一致するとき,液体柱の表面の凸凹が定常波のように見える,この時v = ω k v=\frac{ω}{k} v = k ω
v 2 = ω 2 k 2 = σ ρ k R 0 2 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) (2.2.15) v^2=\frac{ω^2}{k^2}=\frac{σ}{ρkR_0^2}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\tag{2.2.15}
v 2 = k 2 ω 2 = ρ k R 0 2 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) ( 2 . 2 . 1 5 )
また,微小振動の波長はλ = 2 π k = 2 π R 0 k R 0 λ=\frac{2π}{k}=\frac{2πR_0}{kR_0} λ = k 2 π = k R 0 2 π R 0
{ v 2 = ω 2 k 2 = σ ρ k R 0 2 k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) λ = 2 π k = 2 π R 0 k R 0 (2.2.16) \begin{cases}
v^2=\frac{ω^2}{k^2}=\frac{σ}{ρkR_0^2}kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}\\
λ=\frac{2π}{k}=\frac{2πR_0}{kR_0}\\
\end{cases}\tag{2.2.16}
{ v 2 = k 2 ω 2 = ρ k R 0 2 σ k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 ) λ = k 2 π = k R 0 2 π R 0 ( 2 . 2 . 1 6 )
2.2.4. 数値計算
次はPythonを使い式(2.2.15)の描画を行う.修正ベッセル関数の値はscipy.specialで計算する.式(2.2.15)で計算したい未知数はkなので,ここではk R 0 kR_0 k R 0
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) f(kR_0)=kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 )
Pythonのコードは以下である.
from scipy import special
import numpy as np
import matplotlib.pyplot as plt
x = []
y = []
for i in range(100000):
xi=i / 100000
IV1=special.iv(1,xi)
IV0=special.iv(0,xi)
y.append(IV1/IV0 * (1 - xi**2) * xi)
x.append(xi)
plt.plot(x,y)
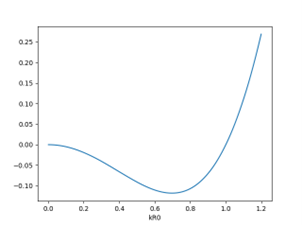
上記のコードで計算を行い、f ( k R 0 ) f(kR_0) f ( k R 0 ) f ( k R 0 ) f(kR_0) f ( k R 0 ) k R 0 = 0.697 kR_0=0.697 k R 0 = 0 . 6 9 7
図5
ω 2 ω^2 ω 2 R ~ \widetilde{R} R
R ~ = R 0 + α e − β t + i k x \widetilde{R}=R_0+αe^{-βt+ikx}
R = R 0 + α e − β t + i k x
β = ∣ ω 2 ∣ β=|ω^2 |
β = ∣ ω 2 ∣
よって,この時のR ~ \widetilde{R} R k R 0 = 0.697 kR_0=0.697 k R 0 = 0 . 6 9 7
次はω 2 > 0 ω^2>0 ω 2 > 0
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 1 ( k R 0 ) I 0 ( k R 0 ) f(kR_0)=kR_0(k^2R^2-1)\frac{I_1(kR_0)}{I_0(kR_0)}
f ( k R 0 ) = k R 0 ( k 2 R 2 − 1 ) I 0 ( k R 0 ) I 1 ( k R 0 )
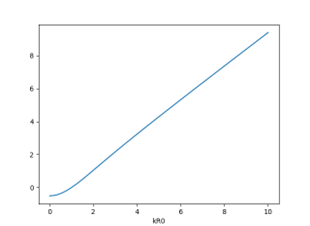
図6
図6を観察すると,関数曲線が直線y = x y=x y = x k R 0 kR_0 k R 0 f ( R 0 ) = k R 0 f(R_0)=kR_0 f ( R 0 ) = k R 0
λ = 2 π k = 2 π σ ρ v 2 (2.2.18) λ=\frac{2π}{k}=\frac{2πσ}{ρv^2}\tag{2.2.18}
λ = k 2 π = ρ v 2 2 π σ ( 2 . 2 . 1 8 )
3. 実験
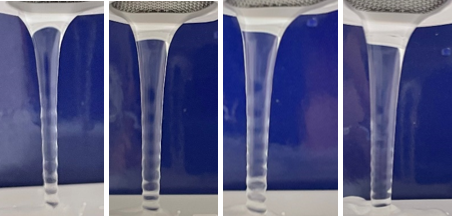
図7
図7は高さを一定にして流量だけを変えて撮った実験写真である(高さ5cm).この時,液体が落ちるは一定であるため,流速が一定と考えられる.図を観察すると,液体表面の微小振動の波長は流量・断面半径と関係ないことがわかる.
次は実験数値を代入して式(2.2.18)を検証する.
v 2 = 2 g h v^2=2gh
v 2 = 2 g h
λ = 2 π σ ρ v 2 λ=\frac{2πσ}{ρv^2}
λ = ρ v 2 2 π σ
よって,λ = π σ ρ g h = 0.46 m m λ=\frac{πσ}{ρgh}=0.46mm λ = ρ g h π σ = 0 . 4 6 m m
4. おわりに
今回の研究では,自由落下流体柱の振動現象についての物理のモデルを解析し,Pythonを使い数値計算を行った,その結論は以下となる.
解析解:式(2.2.17) ,近似解:式(2.2.18) .
今回は蛇口から出る水流を対象として分析を行ったが,この現象は他の流体でも起こっている.この現象の液体の表面張力と液体自身の運動量が原因となっているもので,表面エネルギーと質量がある流体はすべてこれと似た現象があると考えられる。しかし,今回の計算は液体の粘性が含まれていないため,オイルなどの粘性がある流体の現象を正確に計算するには別の解析が必要となる.
参考文献
[1] Wada, Yoshimasa. On the Steady Surface Ripples of a Cylindrical Flow. Journal of the Physical Society of Japan, 5(4), 259–262, (1950). doi:10.1143/jpsj.5.259
[2] Rayleigh, L. On The Instability Of Jets. Proceedings of the London Mathematical Society, s1 10(1), 4–13, (1878). doi:10.1112/plms/s1-10.




Comment