Pytorch tutorials【こちら】
実験で使ったコードは【こちら】
1.はじめに
機械学習が学習を行う際、
「損失関数」と「勾配」からパラメータを更新し、
モデルの最適化を目指しており、
そのために様々な最適化手法(Optimizer)は方法が考案されている
今回はPytorch勉強会をきっかけに現在主流のOptimizerを紹介し、
アルコリズムを理解した上で適用範囲・性能を比較する
2.最適化のアルコリズム
シンプルな関数で最適化を可視化
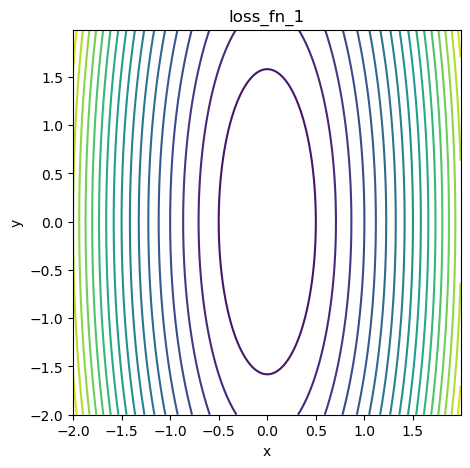
図1 関数の等高線図
各最適化手法における可視化グラフは以下となる
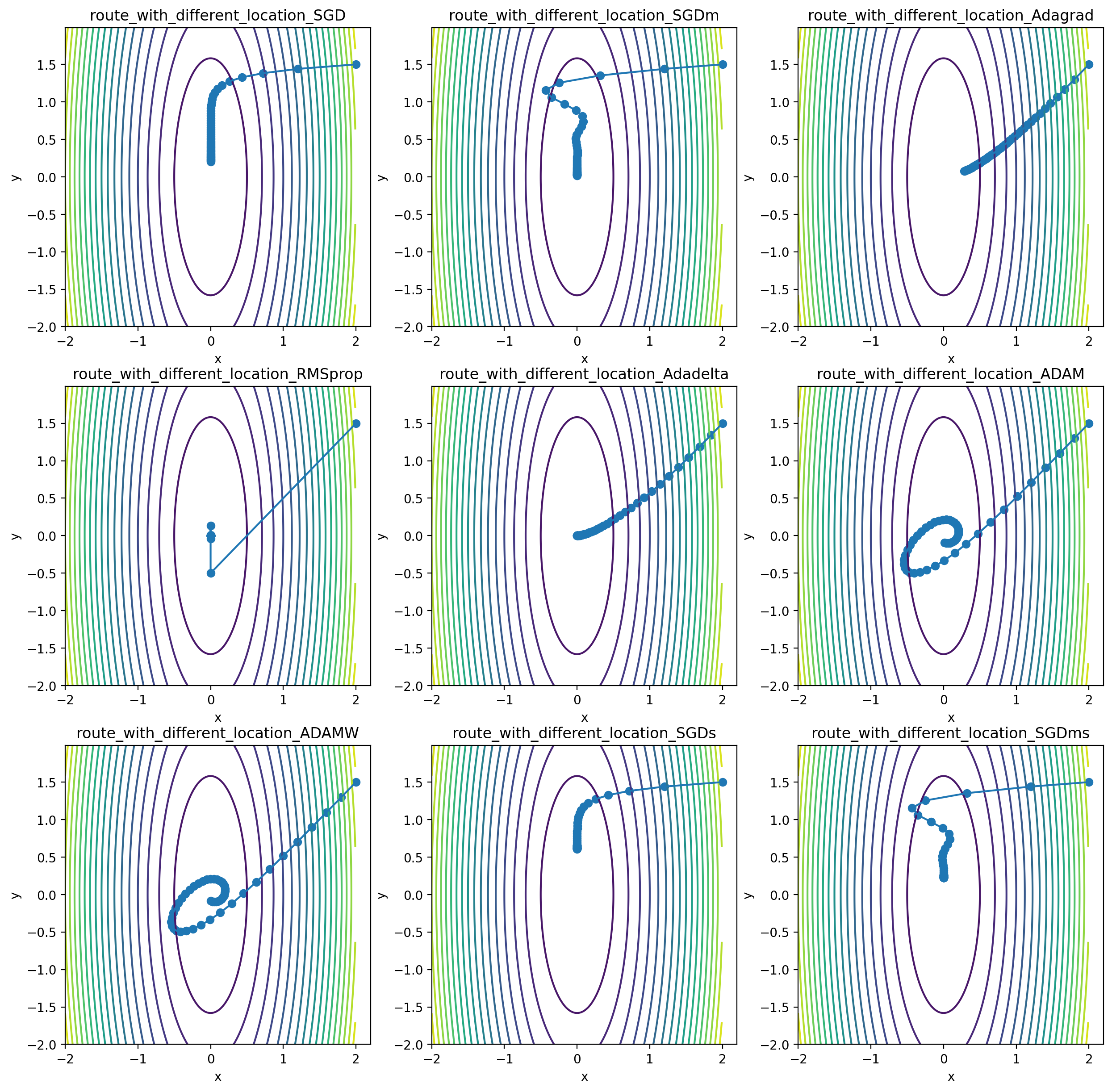
図2. (1-9)
1. SGD
- 求めた勾配方向にその大きさを比例してパラメータを更新する
~ 学習率
~ パラメータ
~ その点の勾配
- しかしステップの長さが決められていることにより、
パラメータが関数の底に飛び跳ねて収束しないことが起こりうる
2. SGD with momentum
- SGDの上に運動量(慣性項)を導入し、
ボールが関数平面上に転がっているイメージでパラメータを更新する
- 図2.2から見ると、降下ルートがOver-shootしていることがわかる
3. AdaGrad
-
学習率を学習過程の中で更新する
-
は更新された学習率であり、
その値の大きさは学習が進むとともに小さくなる -
大きく更新されたパラメータの学習率は、より小さく調整される
-
は勾配の二乗和であり、すべての勾配情報を記録している
-
その欠点も明らかであり、
学習が進むと、が仕方なく大きくなり、
いずれ学習率が非常に小さくなり更新されなくなる -
図2.3も他と比べて同ステップ数の収束が遅れていることがわかる
4. RMSprop
-
AdaGradの問題点を改善するために、RMSpropが提案された
AdaGradと比べて、RMSpropは古い勾配情報を落とし、
新しい勾配情報がより反映されるように記憶している -
の挙動はの畳み込み積分と似ている
- 図2.4がよく収束していることがわかる
5. AdaDelta
-
ほとんど最適化手法は、単位が整っていません
勾配とパラメータでは単位が異り、
更新式の中で単位の違いは特に考慮されていない。 -
その結果、パラメータが勾配の単位で更新される
よりAdadeltaは、単位が整うように
AdagradとRMSprop改良したものになる。
- 式(2.5)により、Adadelta は学習率は存在しません
しかしPytorchは便宜上、Adadelta によって決定された学習率の
スケールするためのパラメータをLrとして残している。
Lr=1 とすれば論文と同じアルゴリズムになる。
6. Adam(Adaptive Moment Estimation)
-
AdamはMomentumとAdagradの融合というアイディアにより提案されている
その更新式は勾配を記憶するMomentumと、
勾配の二乗を記憶するAdagradの項により構成 -
新しい情報がより反映されるように記憶する仕組み
RMSpropと同様
- 図2-6から、まずはMomentumによりボールが転がるような動きをする、
学習率が調整されるとともに、
振れ幅は小さくなりゼロに近づいていく
7. AdamW
- Adamをさらに重み減衰を加える(L2 正則化項)
- 経路はAdam同様に蛇行している、
しかしAdamWの方の経路がより短い
その他の特殊な扱い方
-
N epochごとに減衰させる(pytorchチュートリアル)
-
- 図2-8. SGDに減衰を追加
-
- 図2-9. SGD with momentumに減衰を追加
-
-
- SGDの欠点(飛び跳ねる問題)は回避できたが、
減衰の速度が大きすぎると収束より先に学習率が下がりすぎて動けなくなる
- SGDの欠点(飛び跳ねる問題)は回避できたが、
-
局部最小値のある関数の収束はどうなる?
局部最小値がある関数
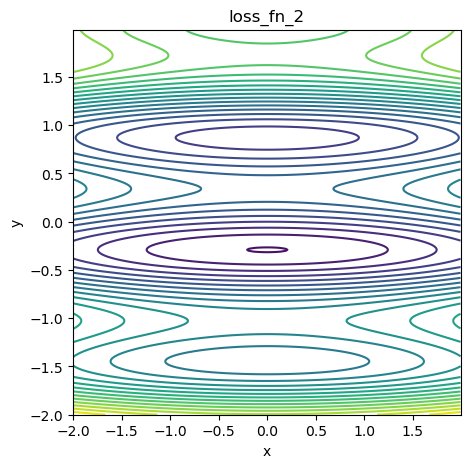
図3 局部最小値がある関数の等高線図
実験
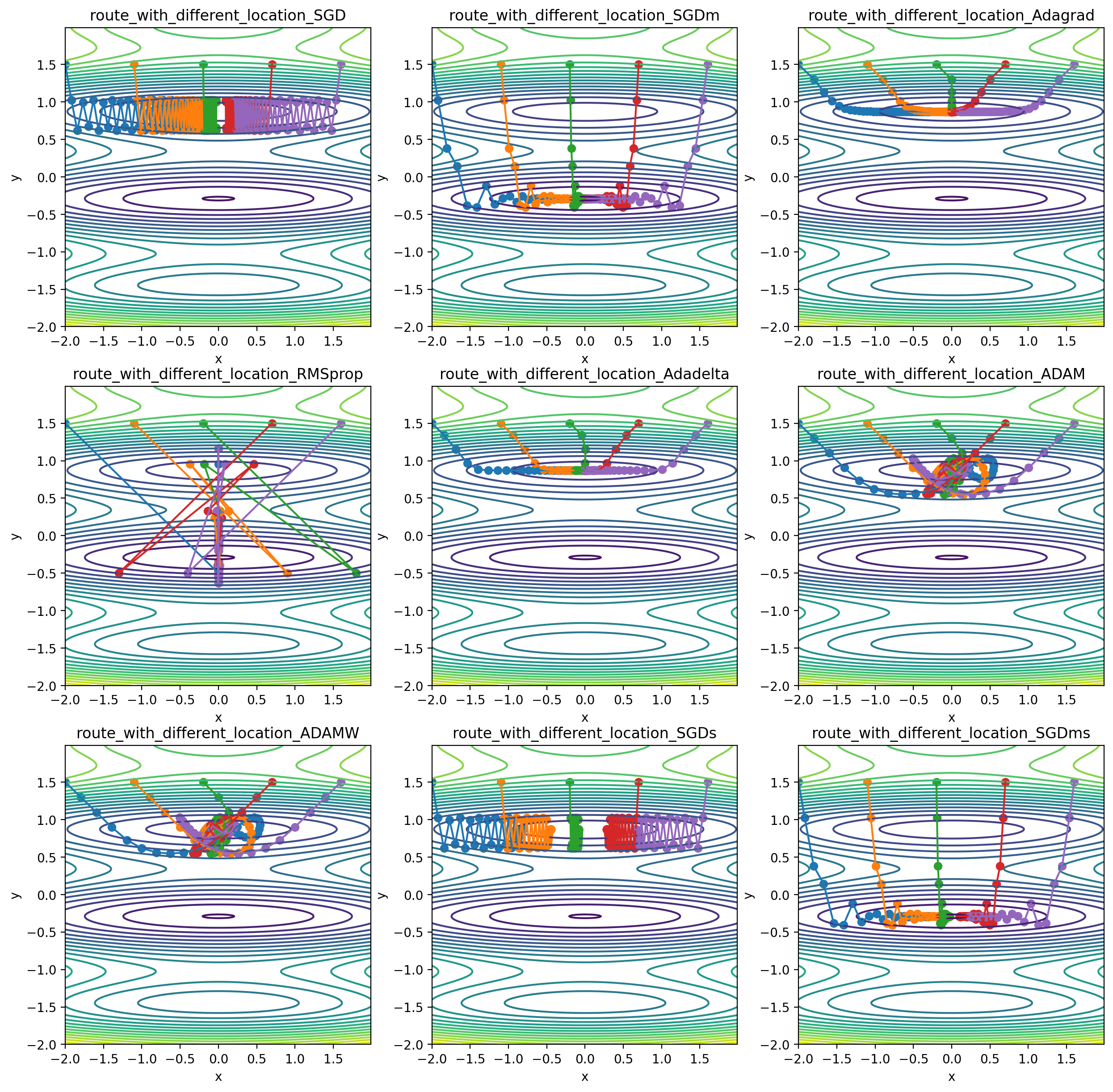
図4 (1-9)
-
モーメントにより支配されると検索範囲が広がる
より遠い極値に到達できる -
RMSpropは初期学習率が高いため遠いところまで到達できる
各最適化手法がLrに対する許容度
(Adadelta は学習率が含まれていないため除外)
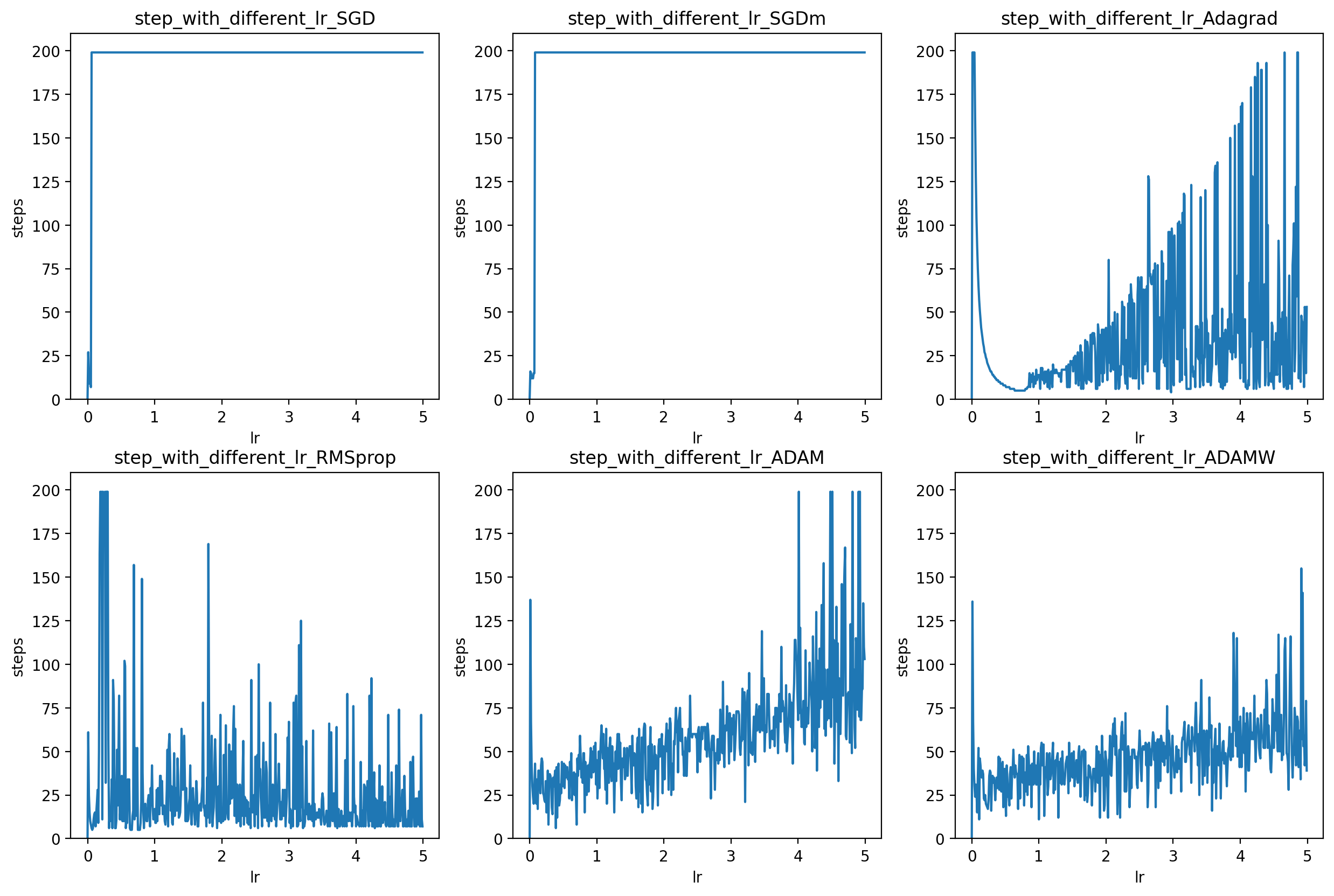
図5 (1-6) Lr[0, 5]
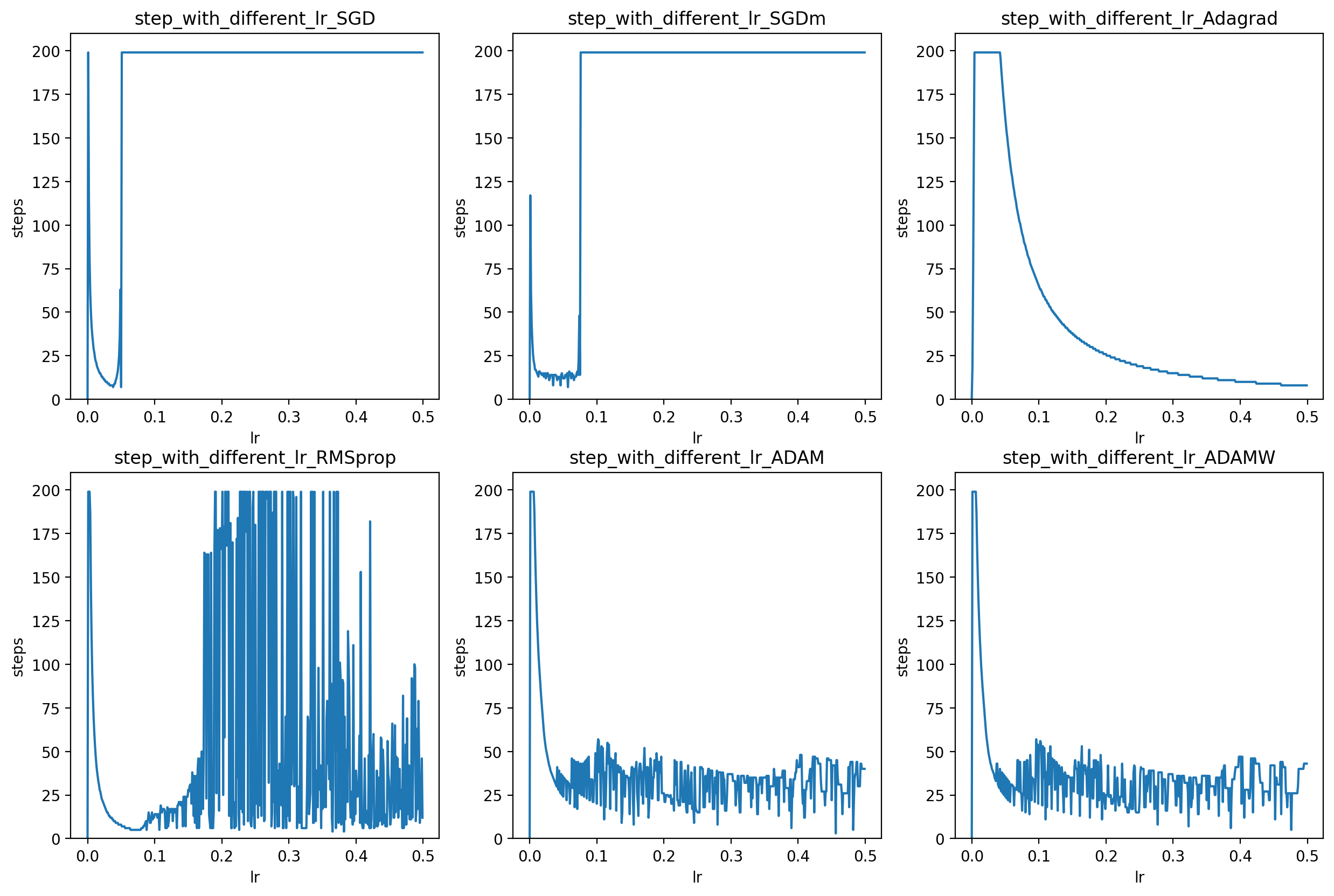
図6 (1-6) Lr[0, 0.5]
- SGDのLr許容度が低い
しかしモーメント項を追加することで少し改善
その他の補足
.backward()は普段の授業でも便利!?
torch.set_grad_enabled(True):
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x.pow(2).sum()
y.backward()
print(x.grad) #tensor([2., 4., 6.])
ResNet(残差ネットワーク)とは
-
CNN の層を深くすると、勾配消失、劣化問題が発生しやすくなり、学習が難しくなる。
これらの問題に向けて ResNet が考案された。 -
Shortcut Connection
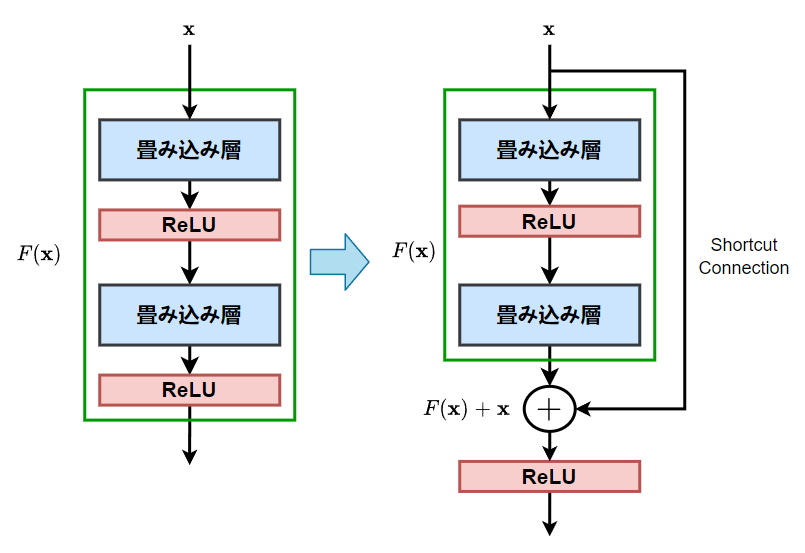
図7 Shortcut Connection
- 構造
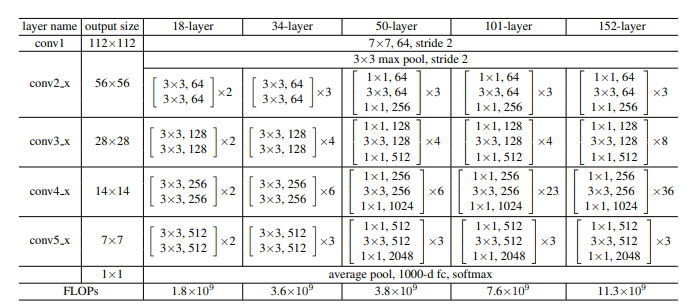
図8 構造
- 残差ネットワークは生物工学的な啓発はないが、
今年(2023)の研究[1]によると、生物(昆虫)の脳にでも残差メカニズムが発見されたという。
CrossEntropyLoss
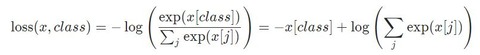
図9 CrossEntropyLoss
#正解データ
y = torch.tensor([3])
#ニューラルネットワークの出力
x_ok = torch.tensor([1, 0.5, 0.5, 2, 0.1 ])
x_ng = torch.tensor([0.5, 2, 0.5, 0.1, 0.8 ])
#softmaxをとって確率密度(.sum()=1)の形にする
x_sm_ok = x_ok.softmax(0)
#tensor([0.1873, 0.1136, 0.1136, 0.5092, 0.0762])
x_sm_ng = x_ng.softmax(0)
#tensor([0.1176, 0.5271, 0.1176, 0.0788, 0.1588])
#x_sm_ok.size() = (batch_size,class_size)にする
x_sm_ok = x_sm_ok.unsqueeze(0)
x_sm_ng = x_sm_ng.unsqueeze(0)
cel=nn.CrossEntropyLoss(reduction="sum")
ok_loss = cel(x_sm_ok, y)
ng_loss = cel(x_sm_ng, y)
print('torch交差エントロピー誤差')
print('出力がokの場合 : {:.3f}'.format(ok_loss))
print('出力がngの場合 : {:.3f}'.format(ng_loss))
#torch交差エントロピー誤差
#出力がokの場合 : 1.314
#出力がngの場合 : 1.745
Fine-tuning と転移学習(Transfer-learning)
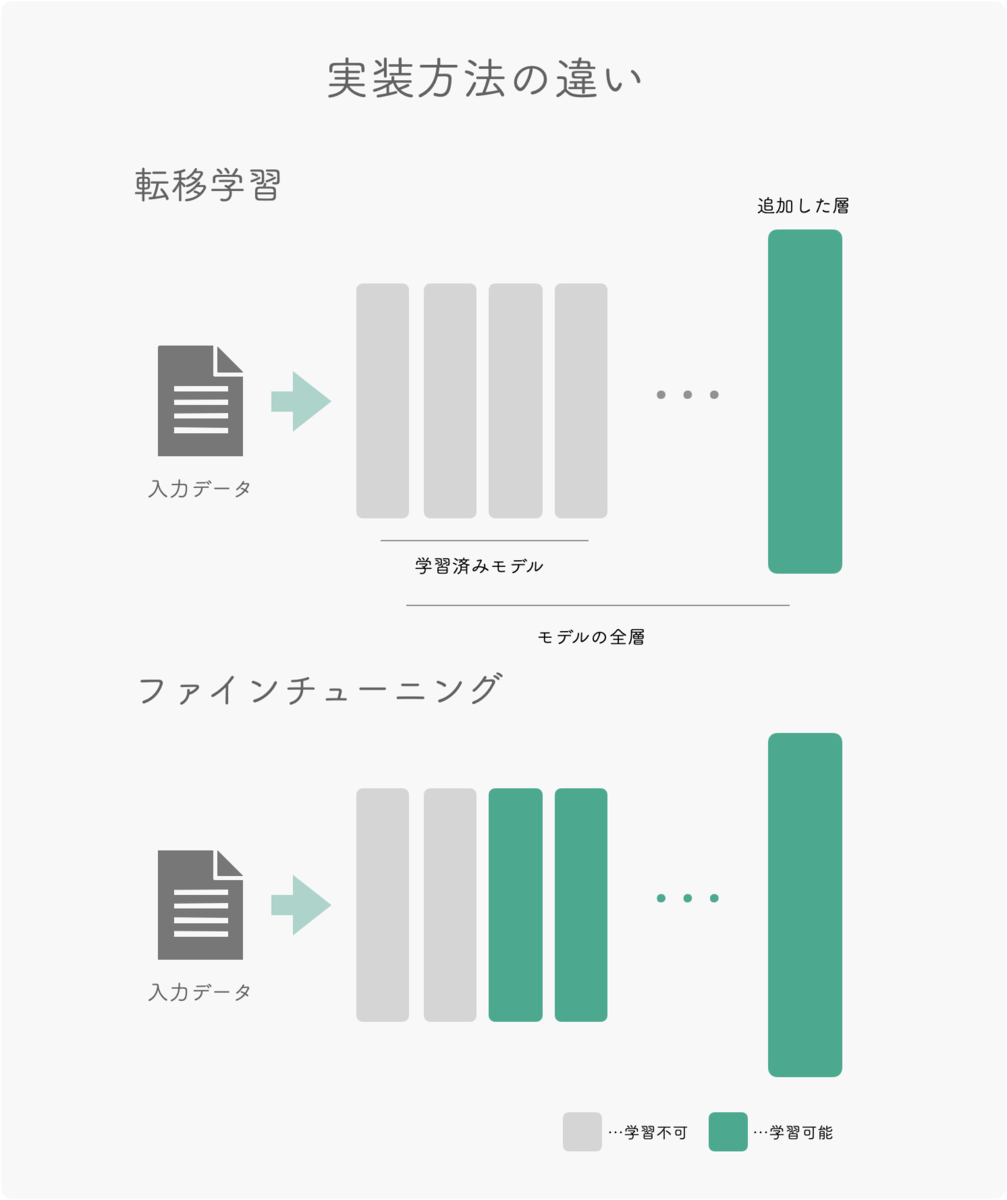
図10 Fine-tuning と転移学習
-
ファインチューニング:
ランダムな値の代わりに訓練済みのパラメータを、ネットワークの初期値として利用する。
訓練済みのパラメータを初期値として使う点以外は、通常通りにネットワーク学習と同じ。
しかし最近では先端からいくつかの層の重みの更新を行わない手法がよく使われている。 -
転移学習(Netを特徴量抽出器として使う) :
最後の全結合層を除いて訓練済みネットワークの重みを固定する。
次に最後の全結合層のみをランダムな重みを持つ新たなものに置き換え、最終層だけを学習する。
参考
- Winding, Michael. et al. (2023). “The connectome of an insect brain”. Science. 379 (6636): eadd9330.




Comment