今回のコードは【こちら】
Denoising Diffusion Probabilistic Models【こちら】
ひとことまとめ
- GANと比べて、一つのモデルしかない
- 情報からノイズ、ノイズから情報へ
- 学習過程(FP)と生成過程(RP)はマルコフ連鎖で決まれ
- 数学的完備
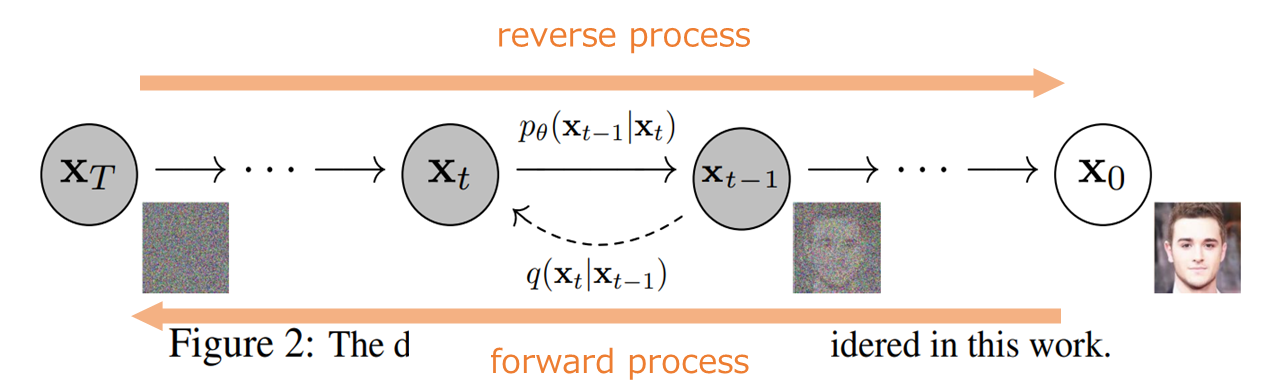
図0
Forword Process
実画像にノイズを加えていく、その過程はマルコフ連鎖で定義されている。
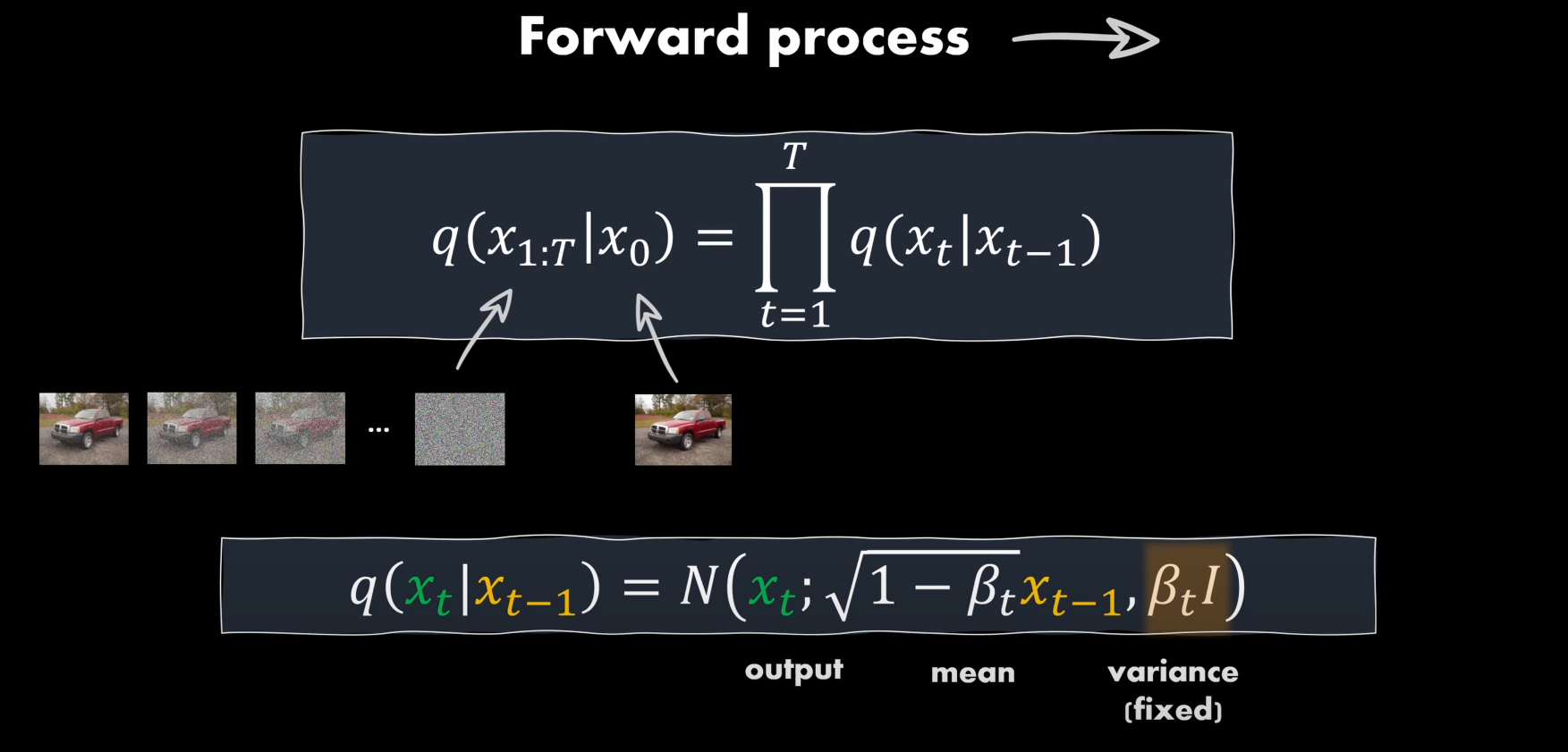
図1
{qθ(X1:T∣X0):=∏q(Xt∣Xt−1)qθ(Xt∣Xt−1):=N(Xt;1−βtXt−1,βtI)(1)
ここでのβtは加えたノイズの強さと考えてよい
二つのガウス分布N(0,σ12I) N(0,σ22I)を足し合わせると新しいガウス分布N(0,(σ12+σ22)I)になることにより
at=1−βt
Xt⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧=atXt−1+1−atϵt−1=at(at−1Xt−2+1−at−1ϵt−2)+1−at−1ϵt−1=atat−1Xt−2+1−atat−1ϵt−2=...=atX0+1−atϵ(2)
つまり
q(Xt∣X0)=N(Xt;atX0,(1−at)I)

図2
よって、t時の画像の状態はX0, tだけに依存する
(あとスケールを決めるハイパラだけ)
これで何がうれしいか?
Reverse Process
途中時刻tの画像のノイズを予測し、ノイズを抜いていく過程。
これもマルコフ連鎖で定義されている。
Xt−1→Xt−noise
⎩⎪⎪⎨⎪⎪⎧qθ(XT)=N(Xt;0;I)qθ(X0:T∣X0):=q(xT)∏qθ(Xt−1∣Xt)qθ(Xt−1∣Xt):=N(Xt−1;μθ(Xt,t),Σ(Xt,t))(3)
- μθ(Xt,t)でネットワークを使う
可能条件について厳密な証明はあるが、証明が難しいため一旦とばす。(DDPM P12-A)
Choose a network
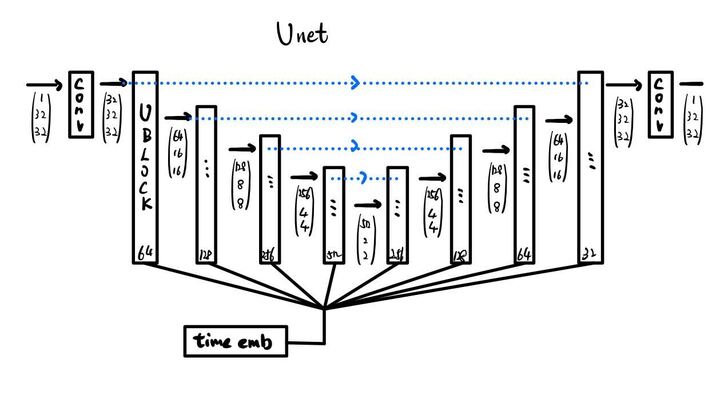
図3-1
UNet!です
- 入力:
t時刻の画像
- 出力:
t時刻の画像のノイズ
- 損失/目的関数
予測ノイズと実際ノイズのL2正則
厳密な証明はあるが一旦とばす。(DDPM P12-A)
しかしこれだけじゃ足りない!
ノイズの強さは時刻によるものなので、時刻のembeddingが必要。
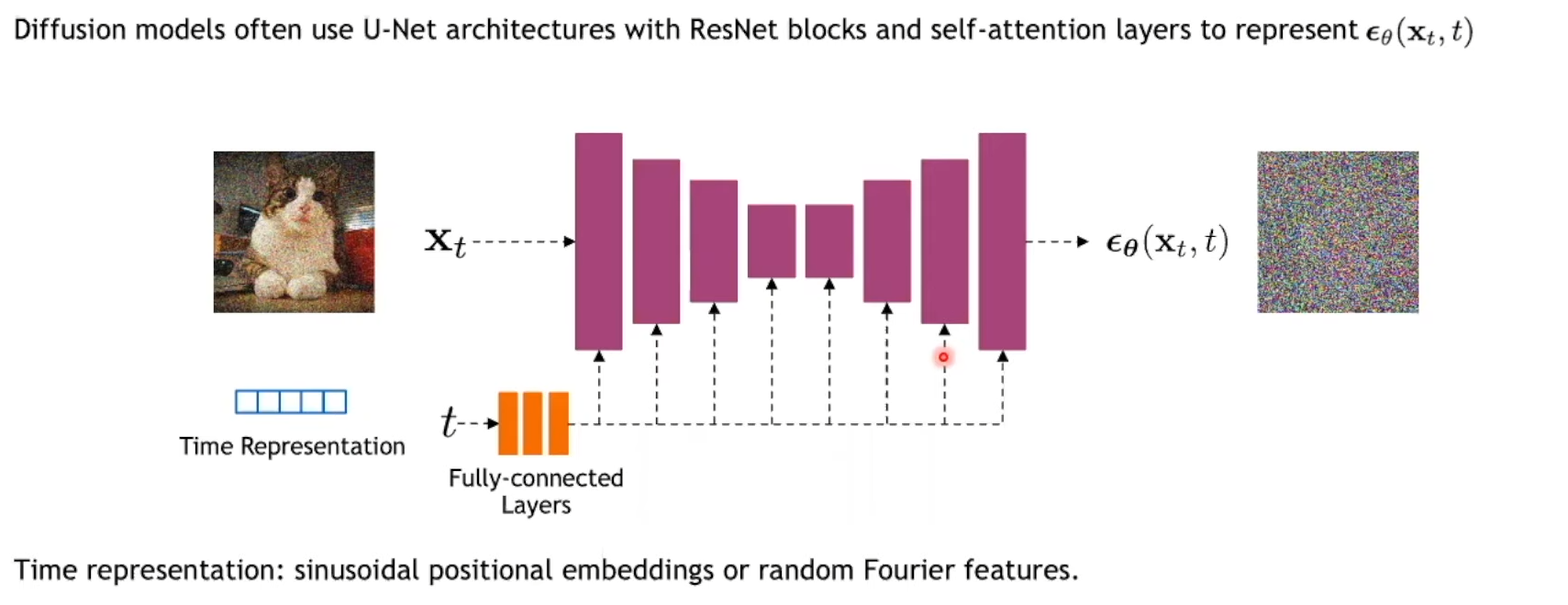
図4
- ここで使ったembeddingはposition embedding
- transformerでも使われている
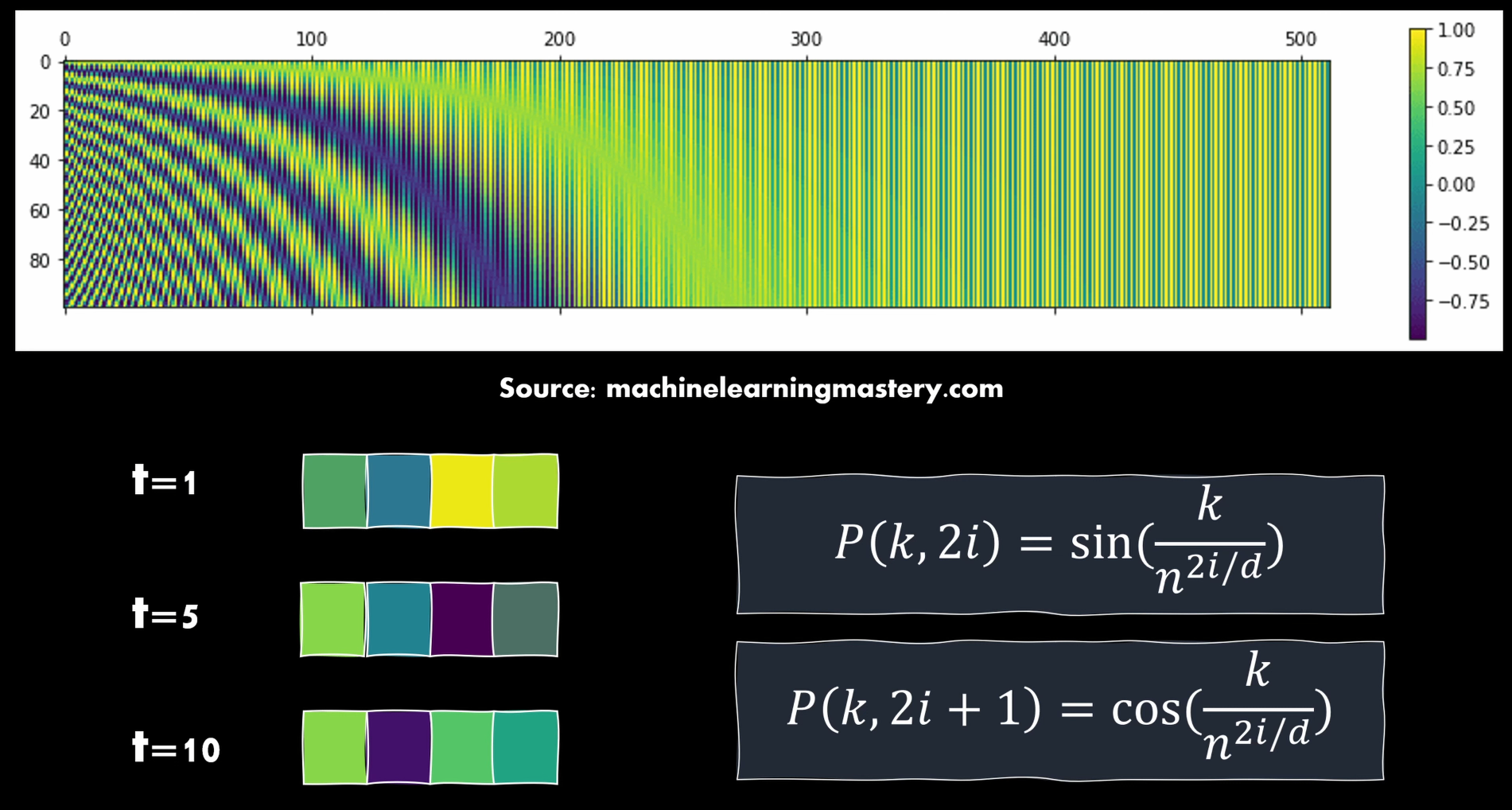
図5
k ~ 位置情報
i ~ i番目のパラメータ
d ~ dimension
n ~ 定数・Attention is all you needでは10000
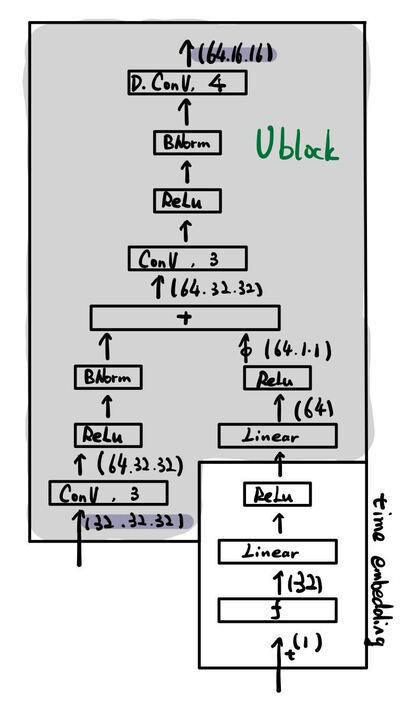
図6
流れのまとめ

図7
実際まわしてみよう!
今回のコードは【こちら】
参考
Understanding Diffusion Models: A Unified Perspective: https://arxiv.org/pdf/2208.11970.pdf
Diffusion models from scratch in PyTorch: https://www.youtube.com/watch?v=a4Yfz2FxXiY
Tutorial on Denoising Diffusion-based Generative Modeling: Foundations and Applications: https://www.youtube.com/watch?v=cS6JQpEY9cs
Positional Embeddings: https://machinelearningmastery.com/a-gentle-introduction-to-positional-encoding-in-transformer-models-part-1












Comment